Aktuelle Seite: Startseite > Schwerpunkt > Berichte > 06 Messtechnik - Teil 2/Aufbau diverser Interferometer > F110C * Induced Astigmatismus an einem KugelSpiegel als Antwort auf Dave Rowe.
F110C * Induced Astigmatismus an einem KugelSpiegel als Antwort auf Dave Rowe.
Der folgende Bericht setzt sich erneut mit dem Thema "Induced Astigmatismus" beim Bath-Interferometer auseinander, weil besonders bei einem
großen Öffnungs-Verhältnis des Licht-Kegels, Astigmatismus "induziert wird, was unter anderem besonders mit dem Bündel-Abstand zu tun hat, wie
er beim Bath-Interferometer im Aufbau entsteht. In meinem Fall wären das 5 mm Bündel-Abstand. Bereits 2004 hat sich Dave Rowe dankenswerter-
weise mit dem Astigmatismus-induzierten Problem in einem eigenen Bericht auseinandergesetzt, wobei im Bericht selbst einige Unklarheiten sind und
ich im vorliegenden Fall das Thema mit meßtechnischen Möglichkeiten zu ergründen versuche. Auch dieses Verfahren ist nicht ganz "scharf", zeigt aber
die Differenzen auf zwischen der mathematischen Formel von Dave Rowe und dem Meß-Versuch an einem KugelSpiegel 150 R 611.
Die mathematische Lösung nach Dave Rowe:
Für diesen Fall ist D=150mm, d=5 mm, R=611 und Lambda 532 nm wave. ODP = 0.289712532 oder PV L/3.45
Der hier induzierte Astigmatismus ist im Zernike System Z4 und Z5, also nur low order und nicht Astigmatismus high order.


Das ist also der Kugelspiegel, dessen Daten in die obere Formel eingesetzt worden waren. Nach der Rechnung würde bei 532 nm wave ein Astigma-
tismus in der Größe von PV L/3.45 eingeführt werden bei einem IMeter-Bündelabstand von 5mm und einem Lichtkegel von ca. F/4 (611/150mm)
Die meßtechnische Lösung
Der Kugelspiegel wurde also a) in Pos_0 = PV L/5.1 Astigm vermessen und b) in Pos_1 +90° clockwise = PV L/7.1 Astigm vermessen.
Der Kugelspiegel-eigene Astigmatismus liegt demnach bei ca. PV L/17.5 bei 532 nm wave.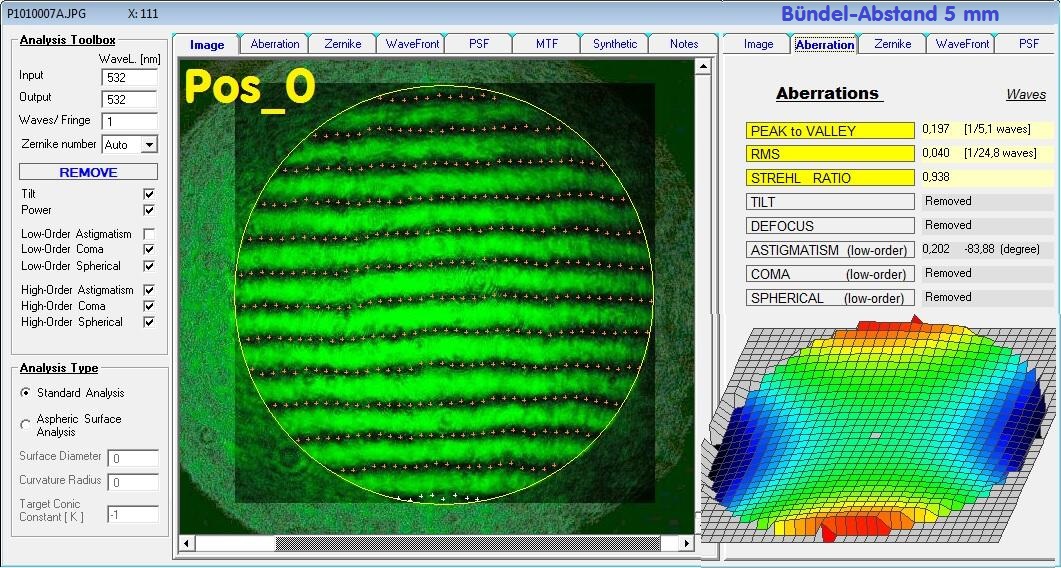
Der Kugelspiegel-eigene Astigmatismus beläuft sich also auf die Differenz zwischen PV L/5.1 und PV L/7.1, sodaß für den induzierten Astigmatismus
bei Bündelabstand 5 mm bei einem Lichtkegel von ca. R/4 ein Wert von ca. PV L/6 übrigbleibt. Das wäre aber gegenüber dem math. Wert von PV L/3.45
ein etwas kleinerer Wert, der deswegen eher stimmen könnte, weil er meßtechnisch zustande kam. Die mathematische Lösung müßte man nämlich
beweisen.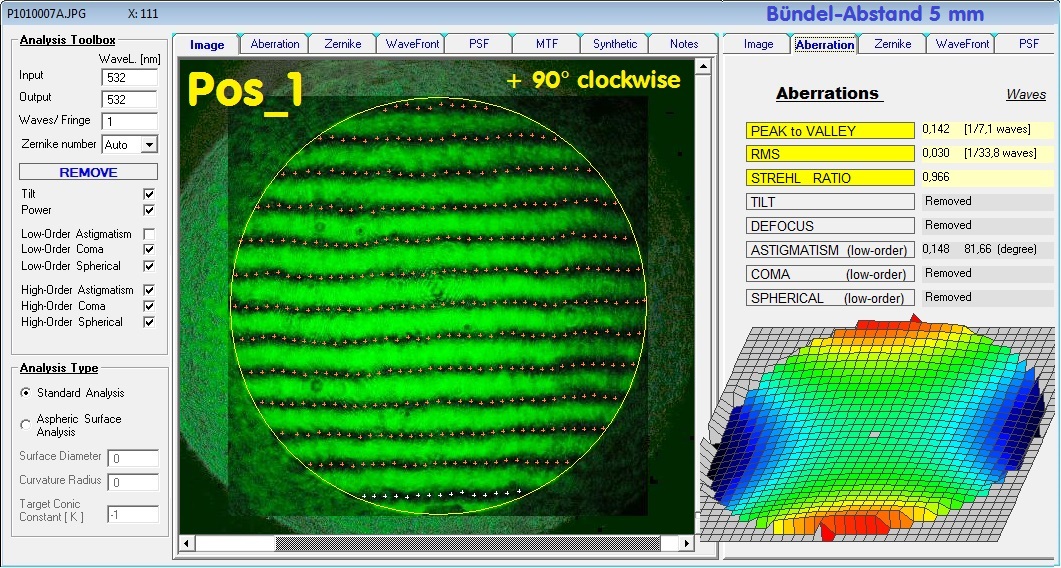
Für den nachfolgenden Versuch ist es besser, wenn man ein simulierten Interferogramm mit den Werten für Astigm. PV L/5.1 und PV L/7.1 hat. Es soll
nämlich die Situation an schmäleren LichtKegeln untersucht werden, also nach R/4 auch R/5, R/6 und R/8 wegen der Frage, wie massiv sich dieser System-
oder Setup-Fehler beim Bath-Interferometer auswirkt. 
Der jeweils kleinere Umkreis steht auch für ein kleineres Öffnungsverhältnis bzw. schlankeren Lichtkegel. Wenn man also besonders bei F/4 Newton-
Spiegeln "ausweichen" will, dann empfiehlt sind eine Prüfung auf Astigmatismus in RoC, da hätte man dann einen F/8 Lichtkegel und in Autokollimation
kann man dann nur auf sphärische Aberration prüfen, und so diesen Effekt ebenfalls umfangen. Prüft man hingegen "schnelle" Refraktoren, dann ist
ein F/6.56 Öffnungsverhältnis ebenfalls unkritisch.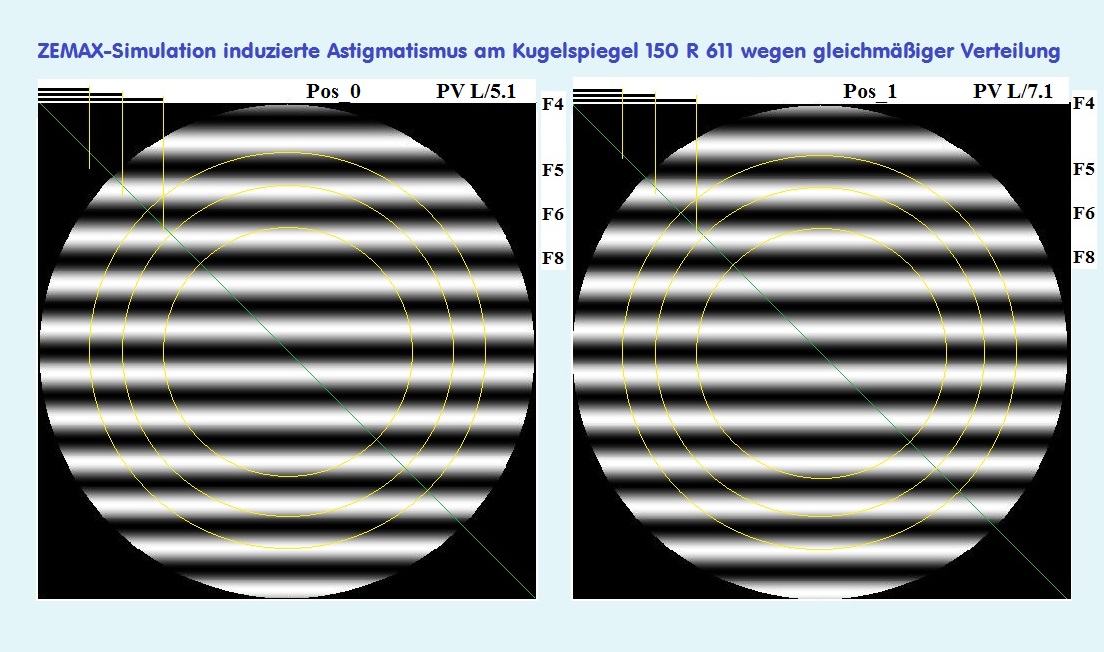

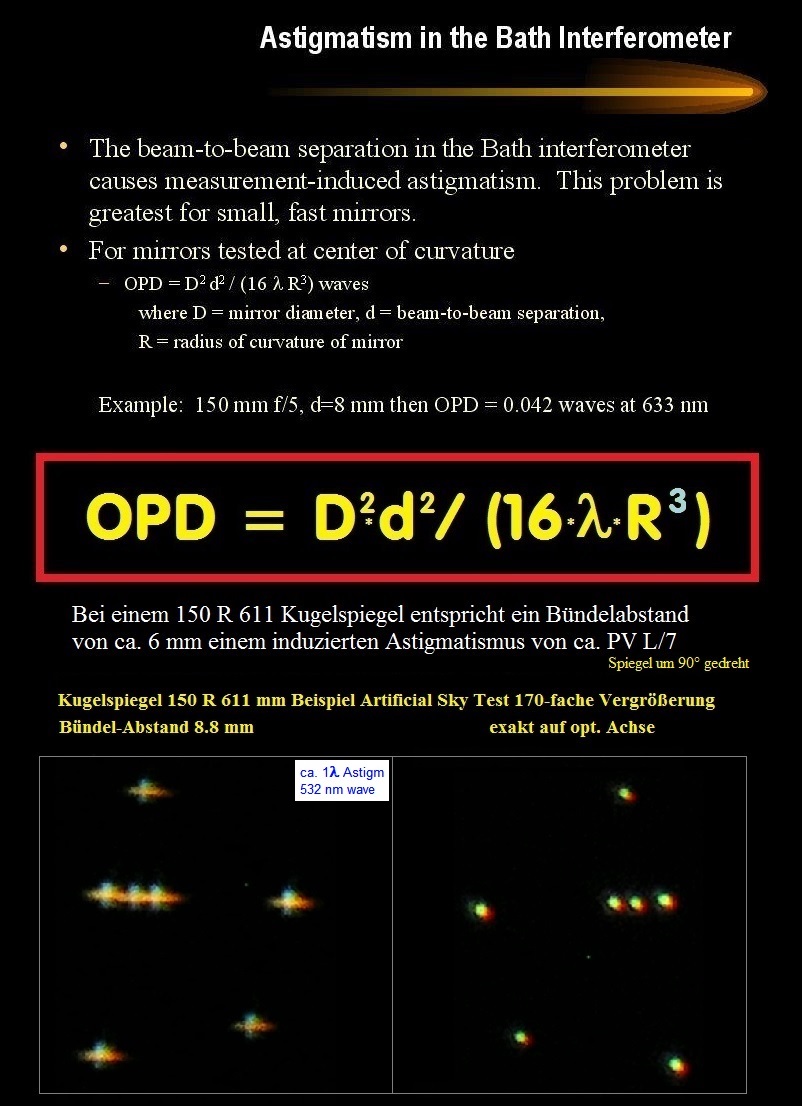
Der gleiche Effekt zeigt sich im übrigen beim Artificial Sky Test bei hoher Vergrößerung: Auch hier wird über den "Bündel-Abstand" von 8.8 mm
ein Astigmatismus induziert, weshalb man für große ÖffnungsVerhältnisse exakt auf der opt. Achse prüfen muß:
exakt auf der opt. Achse http://rohr.aiax.de/VFW_05A.png bis zu einem Lichtkegel von f6 http://rohr.aiax.de/RicRed_04.jpg

Kommentare
Bei R/6 entsteht ein Astigm von PV L/7.46
Bei R/8 entsteht ein Astigm von PV L/13.4
Bei R/10 entsteht ein Astigm von PV L/21.0
gerechnet über die Formel von Dave Rowe:
OPD = D^2*d^2 / (16 * Lambda * F^3)
Gerechnet über Sphäre 150 F 611; R und F
sind bei diesem Beispiel gleich zu behandeln
D = Durchmesser Optik, d = Bündelabstand
(9mm), Lambda = 532 nm wave
Alle Kommentare dieses Beitrages als RSS-Feed.