10. Oktober 2008

Größe und Genauigkeit eines Fangspiegels spielen bei einem Newton-System eine nicht
unerhebliche Rolle. Dabei gibt es eine Reihe von Faktoren, die zu berücksichtigen sind.

01. Der Abstand Fangspiegel-Fokus muß HS-Spiegeldurchmesser/2 + 150-200 mm. Darin enthalten
ist der Tubus- oder Hut-Außendurchmesser/2 + Fokussierweg.

02. Aus diesem Abstand ergibt sich der Fangspiegel-Mindestdurchmesser für die kleine Achse,
indem man Fangspiegel-Fokus-Abstand durch die Öffnungszahl teilt. In unserem Beispiel 500/4.16
für einem 600/2500 Newton. Das wäre eine kleine Achse von ca. 120 mm. Mit 1.414 multipliziert
erhält man die große Achse.
Bei diesem System wäre der 120 mm Fangspiegel das Minimum, außerhalb der Achse hätte man
sofort Vignettierung, man hat also nur auf der Achse selbst die volle Hauptspiegelfläche im Bild.
Visuell mag das gerade noch gehen, fotografisch wäre das in jedem Fall zu klein.

03. Der Hauptfehler bei Fangspiegeln dürfte die Power bzw. Planität sein. Astigmatismus wäre
noch mißlicher. Die Power sollte gegen Unendlich gehen, dann hätte man die Situation, wie sie
das erste Bild zeigt. Bereits ein Radius von 25 km ergäbe etwa einen Fehler von L/4 PV der
Wellenfront. Das stört aber in keinem Fall.

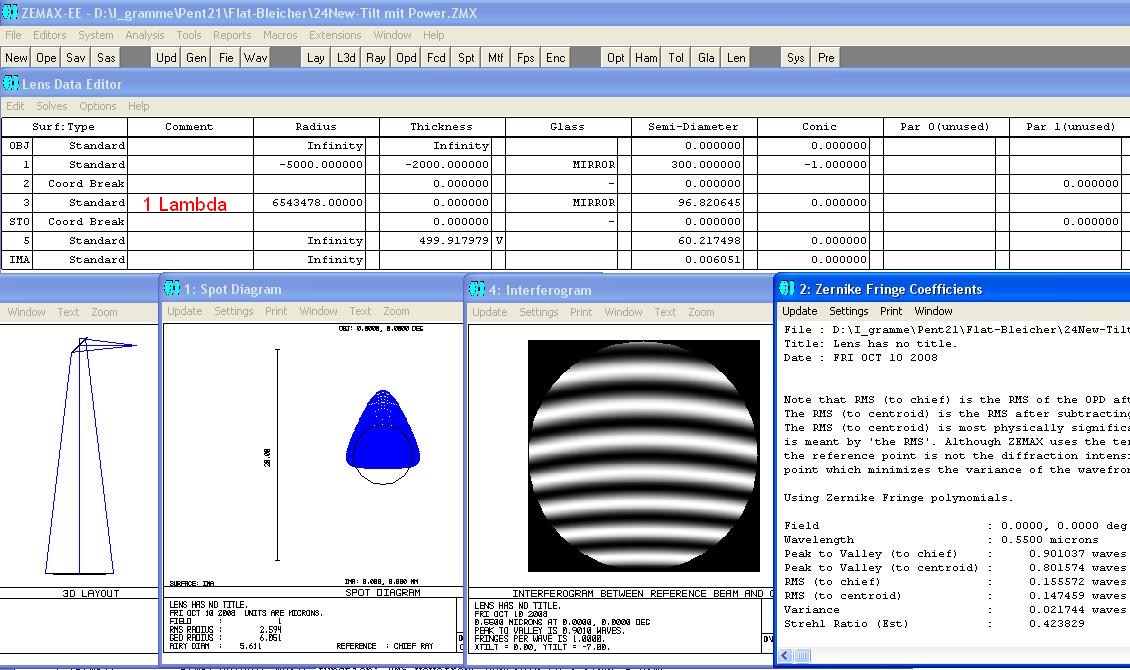
04. Ein Streifenabstand bei der Messung auf Kontakt entspricht 1* Lambda PV der Wellenfront.
05. Alle PV-Angaben entsprechen also PV der Wellenfront, nicht der Oberfläche !!!



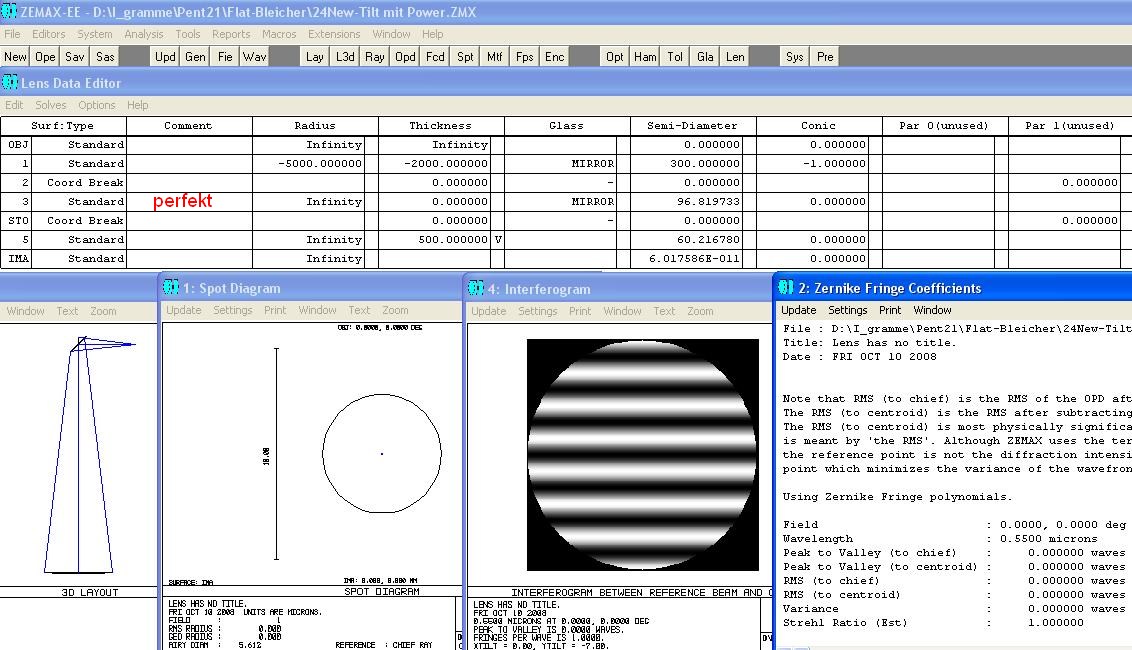
Nun prüft man den Spiegel auf Kontakt und hätte eine Streifendurchbiegung von Lambda/4, vorausgesetzt,
beide Glaskörper haben die gleiche Temperatur, und die Referenzfläche ein eindeutiges Certifikat. Weil man
die Streifen aber entlang der langen Achse gelegt hat zur besseren Einschätzung der Situation wird aus
120 mm der kleinen Achse 169.68 mm große Achse und wir müssen berechnen, welcher Radius auf dem
Planspiegel bzw. Abweichung von der Planität diesem Betrag Lambda/4 bei 550 nm wave entspricht.
Nach der Formel (für die Parabel) wäre der Radius: Halbachse^2/2/Pfeilhöhe. Im Beispiel wäre das
für Lambda/4 Pfeilhöhe: 84,84^2/2/0.0001375 das entspricht einem Radius von 26 173 911 mm
für Lambda/2 Pfeilhöhe: 84,84^2/2/0.0002750 das entspricht einem Radius von 12 829 091 mm
für 1*Lambda Pfeilhöhe: 84,84^2/2/0.0005500 das entspricht einem Radius von 6 543 478 mm

Lambda/4 Planität wäre also völlig in Ordnung, das Spotdiagramm weit innerhalb des Airy-Scheibchens

und der Strehl rechnerisch ohne andere Störungen bei ca. 0.95



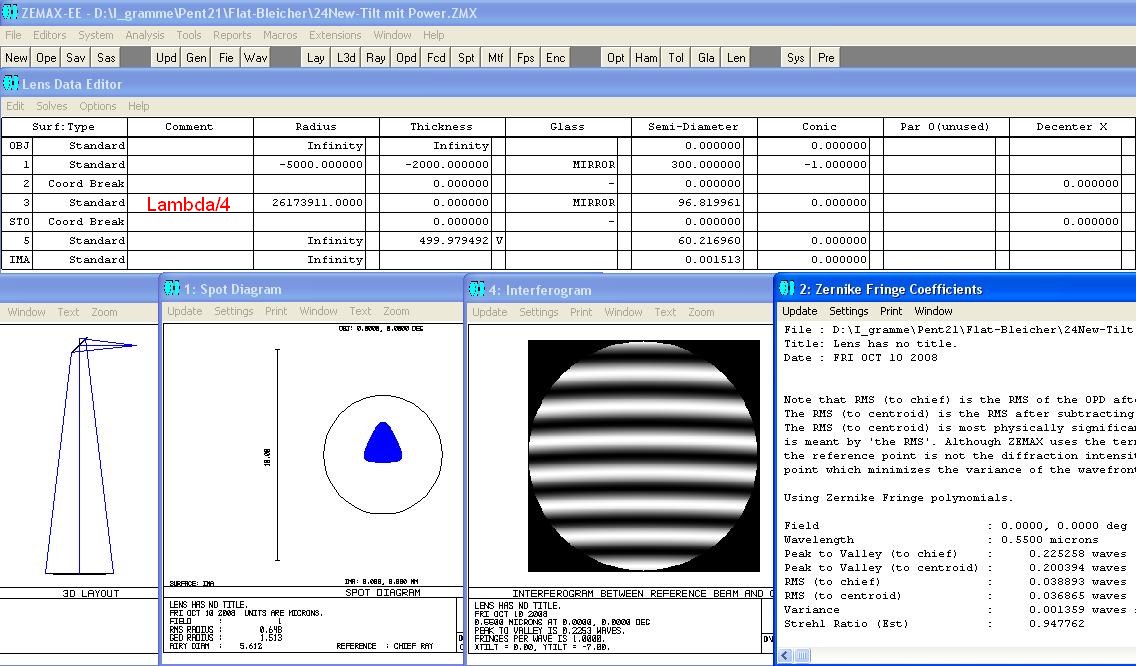
Auch eine Streifendurchbiegung von Lambda/2 liefert für die meisten Fälle noch eine brauchbare Abbildung
ab, da eine Reihe anderer Einflüsse ebenfalls Strehl-mindernd tätig sind. Also ein möglicher Astigmatismus
auf dem Hauptspiegel, die thermischen Einflüsse auf die Korrektur des Spiegels, die Luftunruhe, die richtige
Kollimation des Systems usw. Jetzt wäre rechnerisch das Airyscheibchen noch etwas größer als das Spot-
diagramm und der Strehl im Bereich von 0.80



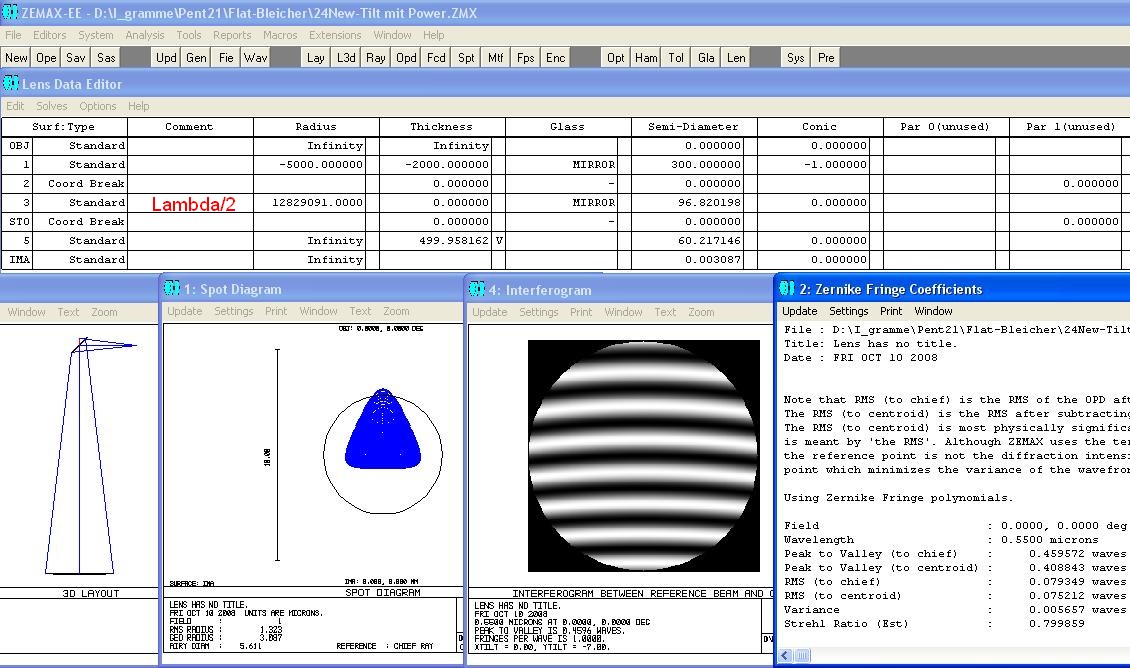
Selbst bei einer Streifendurchbiegung von 1* Lambda wird man noch nicht viel merken, obwohl das Spot-
diagramm nun größe als das Airy-Scheibchen ist. Weil aber das Spotdiagramm eine dreieckige Form hat, ist
das Sternpünktchen 3-eckig verformt, und das wird man kaum wahrnehmen. Die Sternpünktchen sind im
Durchmesser lediglich um einige 2-3 Micron größer. Solange kein anderer Astigmatismus im Spiel ist, der
ein ovales Sternscheibchen erzeugt, das sich im Fokus um 90° dreht, wird man den etwas größeren Stern-
Durchmesser gar nicht merken. Man hat nämlich auch große Mühe einen Astigmatismus von L/3 PV, der
vom Hauptspiegel stammt, im Fokus zu merken. Es gilt also, wie in vielen Fällen, in der Praxis auszuprobieren
ob nach richtiger Lagerung von Haupt- und Fangspiegel über einen Fangspiegel mit Power von bis zu
2*Lambda ein dreieckiger Astigmatismus bemerkt wird. Bei mangelhafte Kollimation stört z.B. die Koma
eines Newton-Systems sehr viel mehr.



Nun gibt es auch noch den Fall, daß der Fangspiegel größer ist, und somit das Certifikat über die
gesamt Fläche ausgestellt ist, obwohl aktuell vom Lichtkegel z.B. nur die Hälfte benutzt wird.
In diesem Fall müßte man die Genauigkeit der GesamtFläche auf die Teilfläche zurückrechnen und
damit nimmt die benutzte Teilfläche an Genauigkeit zu. Einen ähnlichen Effekt erreicht man, wenn
man den Fangspiegel so weit wie möglich in Richtung Fokus schiebt.

Für einen einwandfreien Fangspiegel gilt also etwa L/4 PV der Wellenfront oder L/8 PV der
Oberfläche für die tatsächlich benutzte Teilfläche, und alles andere wäre akademische Diskussion.

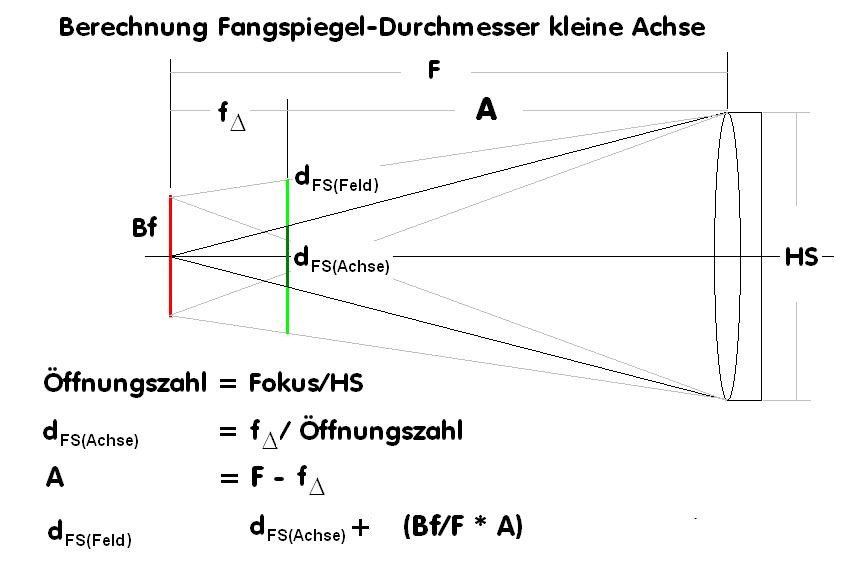
Zur Berechnung des Fangspiegel-Durchmessers,
Zur Berechnung des Fangspiegel-Durchmessers a) auf der Achse und b) für ein Bild-Feld bestimmter Größe
siehe untere Übersicht.

zu a) Den Fangspiegel-Mindest-Durchmesser für die Achse bekommt man, wenn man den FS-Fokus-
Abstand durch die Öffnungszahl teilt, 500/4.1666 = ca. 120 mm (Öffnungszahl = 2500/600 = 4.16666)

zu b) Will man im Fokus einen bestimmten Felddurchmesser frei von Vignettierung erhalten so muß zusätzlich
noch ein Betrag dazuaddiert werden der sich aus der unteren überschlägigen Formel d_FS(Feld) ergibt.
in unserem Beispiel noch 16 mm zu den 120 mm Fangspiegel-kleine-Achse dazu. Ansonsten
muß man Vignettierung in Kauf nehmen, was auch Vorteile hat.