16.06.2005    Abstand künstlicher Stern: Auf den richtigen Abstand kommt es an

Das ist einer der frühen Berichte, nachdem im Januar 2004 unser Forum gegründet worden war.
Bemerkenswert für diesen Bericht ist die Text-Formatierung, die software-bedingt noch sehr kurze
Zeilen damals hatte. Auch die Bildgröße war damals sehr viel kleiner. In diesem Fall lag der Bericht
im Archiv nur noch als Text-File, sodaß ich ihn in dieser ursprünglichen Formatierung nochmals
einstellte - für eine aktuelle Überarbeitung fehlt mir im Augenblick die Zeit.

16.06.2005, 19:07
Aus aktuellem Anlaß habe ich über ZEMAX simuliert, wie sich der Abstand beim
Testen von Newton-Spiegeln auf das Ergebnis auswirkt. Parallel dazu gibt es
auf A.de einen Thread, dessen Abstandsformel einer Überprüfung durch ZEMAX
nicht standhält.

Gehen wir von der Kugel aus. Im Idealfall ist der Öffnungsfehler = 0, der PV-Wert
der Wellenfront liegt bei unglaublichen 1/1000 * Lambda und besser und der
Strehl bei exakt 1.000. Für den Himmel wäre das nichts, außer bei kleinen Öff-
nungen, also bei f/8 und kleiner. Dabei ist aber die Geometrie der Lichtstrahlen
zu beachten: Beim Testen einer Kugel geht von der Pinhole ein Lichtkegel auf
den Kugelspiegel, und wird als Lichtkegel in sich reflektiert zurückgeworfen.
Am Himmel haben wir es aber nicht mit einem Lichtkegel zu tun, sondern mit
einem Parallel-Lichtbündel, was streng genommen ein unendlich schlanker
Lichtkegel ist, wäre die Lichtquelle wieder eine Pinhole. In Wirklichkeit ist es
eine riesige leuchtende Kugel, nämlich der Stern, "unendlich" weit weg, was
ebenfalls nicht ganz stimmt. Aber das Lichtbündel, das benutzt wird, für
unsere Zwecke parallel.

Diese Situation veranlaßt den Spiegelschleifer, aus einer f/8 Sphäre, der am
Himmel ein f/4 Spiegel ist, aber total-Unterkorrigiert, veranlaßt also den
Spiegelschleifer, den Öffnungsfehler der Unterkorrektur durch Vertiefung der
Spiegelmitte wegzuretouchieren, oder zu "parabolisieren". Jetzt stimmt es
für ein paralleles Lichtbündel, aber nicht mehr für den Lichtkegel aus dem
Krümmungsmittelpunkt. Für diesen Lichtkegel ist die Parabel nun total über-
korrigiert. Und so zeigt sich die Überkorrektur dieses 200/800 Newton-
Spiegels im Interferogramm mit dem Bath-Interferometer, d-Linie 587.6 nm
wave, im Krümmungsmittelpunkt, wenn man den Fokus optimiert.

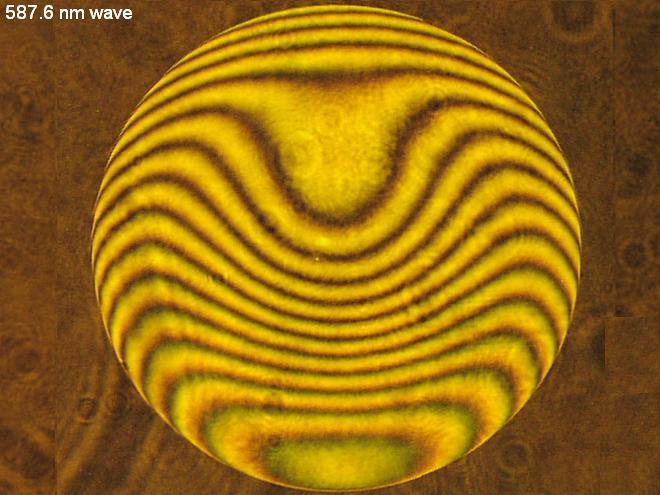
Also setzt man den jetzigen Parabolspiegel vor einen Planspiegel, und hat jetzt
wieder die Situation, wie am Himmel, parallele Streifen mit exakt gleichen
Streifenabständen, was in der Praxis natürlich selten vorkommt.

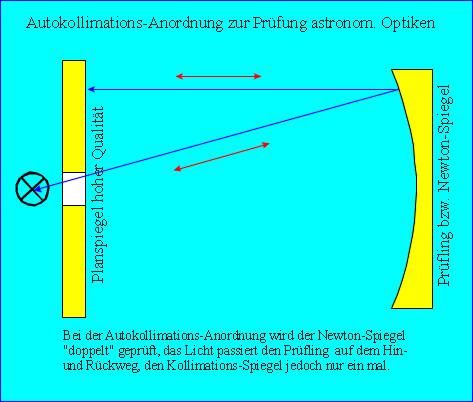
Nun hat aber nicht jeder einen Planspiegel, und versucht es mit einem künst-
lichen Stern. Da bekommt er aber ein Problem: Von der Logik prüft er nämlich
nicht gegen ein Parallel-Lichtbündel, sondern gegen einen Lichtkegel, der je
nach Abstand größer oder schlanker ist. Er wird also mehr oder weniger deutlich
überkorrigierte Sternscheibchen bekommen, weil er sich zwischen dem COC =
Krümmungsmittelpunkt-Lichtkegel und dem parallelen Lichtkegel bewegt. Also
habe ich am Standard-Beispiel eines f/4 200/800 Newton-Spiegels die Sache
mit ZEMAX simuliert bei einem Pinhole-Abstand von leider nur 50 000 mm oder
50 m. (Im Krümmungsmittelpunkt sieht man intrafokal kein Sternscheibchen
mehr, aber einen wunderbaren Lichtwulst extrafokal.)

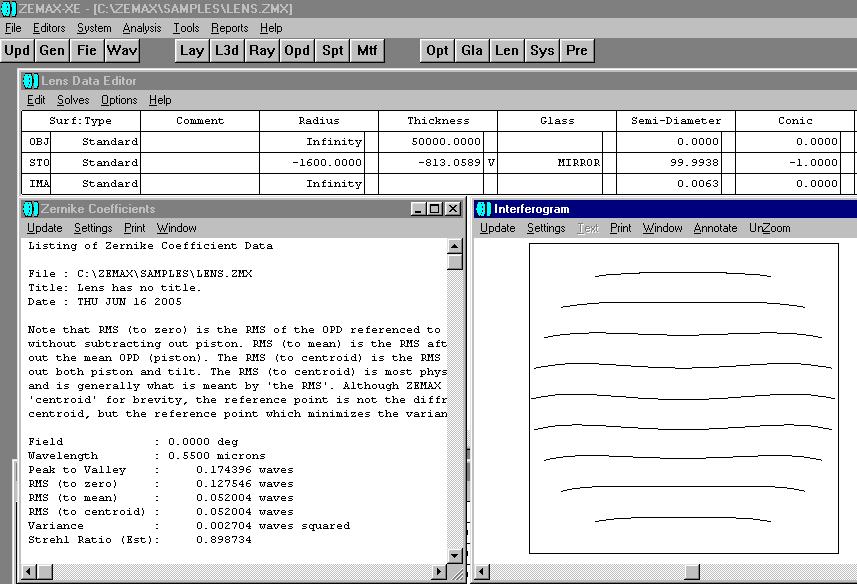
Wenn also jemand mit einem Pinhole-Abstand von 50 m ein solches System
prüfen will, dann sind alle Ergebnisse überkorrigiert, d.h intrafokal ist das
Sternscheibchen ausgefranst und extrafokal hat man außen den deutlichen
Lichtwulst. Umsomehr, wenn der Spiegel entweder eine leicht abfallende
Kante oder vielleicht eine zarte Überkorrektur aufweist, die ebenfalls für
diesen Effekt verantwortlich sind.

Also könnte man leicht glauben, da hat doch der Hersteller, oder vielleicht der
Prüfer ...(dessen Problem häufig ist, daß bei vielen fremden Gegentests zwar
viel behauptet wird, aber die Prüfbedingungen selten bis gar nicht exakt
reflektiert und dargelegt werden, unter denen getestet worden sind. In
diesem Fall z.B. die genaue Angabe des Abstandes Pinhole - Parabolspiegel.)

Für den perfekten und idealen Fall eines 200/800 Newton-Spiegels ohne
weitere Fehler sagt die ZEMAX-Simulation bei den in der Tabelle simulierten
Abständen folgende Ergebnisse voraus. Abstand und Schnittweite jeweils
in mm. Schnittweite ist allgemein immer der Abstand der letzten Fläche
zum Fokus. Bei Spiegelflächen ist das auch der Fokus, bei Linsen-Systemen
oder katadioptrischen Systemen eben nicht.

Im Fall A der Simulation wird die überkorrekturbedingte Strehl-Vermin-
derung durch zu kleine Pinhole-Abstände am Beispiel eines 200/800
NewtonSystems simuliert, und erst beim Abstand von 150 m ist der
Strehl-Verlust nur noch 1 %.

Im Fall B werden für unterschiedliche NewtonSysteme die opt. Abstän-
de simuliert, damit der Strehlverlust nur noch 1 % beträgt. Derartige
Tests sollte man sicherheitshalber immer am Stern, und dann immer
mit dem Ronchi-Test gegenprüfen, weil dieser Test eindeutiger ist.
(Bereits bei abfallender Kante wird der Sterntest nach Suiter unscharf
und ungenau)

Fazit: Einigermaßen sicher für diesen konkreten Fall ist eine Meßstrecke von
100 m und mehr, der künstliche Stern muß für diesen Fall also mindestens
100 Meter Abstand haben, dann liegt man mit 3% Strehldifferenz immer noch
noch daneben, oder sieht einen überkorrigierten Newton-Spiegel, obwohl
der Spiegel eigentlich perfekt korrigiert ist. Also doch der Planspiegel oder der
Himmel/Polarstern. Die Geometrie ist eigentlich einfach, nur weitgehend
unbekannt. Für größere Spiegel wachsen natürlich die Meßstrecken geome-
trisch. Mit AtmosFringe kann man auch CoC-Streifenbilder auswerten, wie
das ein ZYGO aus der Industrie kann. Vorraussetzung jedoch ist, daß man
mindestens auf mm genau die Daten für Durchmesser und Krümmungsradius
eingibt. Das stößt bei manchen schon an die Grenzen ihrer Meßgenauigkeit,
nicht jedoch an ihr Mitteilungs-Bedürfnis.