Hallo Jörg,

zur Auflösung eines opt. Systems gibt es zwei Wege:

A) die theoretische unter Laborbedingungen für nicht obstruierte Systeme

Hierbei gibt man die bekannten opt. Daten ein.



B) die praktische am Stern mit Meßokular oder in Autokollimation

Hier mißt man den Durchmesser einer Sternabbildung und rechnet nach der Formel, wobei
wir hier den Näherungs-Wert eingesetzt haben. Es gilt weiterhin der obere Wert von 206 265" .
Das Cassegrain-System hatte eine deutliche Zone.



weiterführende Literatur:

##########################################################################################

http://www.epsilon-lyrae.de/Seeing/MTF1/ArtikelMTF1.html

Beugungs-begrenzt und Strehl-Wert

Bei der Frage, was man unter "beugungs-begrenzt" versteht (Strehl-Wert>= 0.80) , gibt es hier einige Informationen.
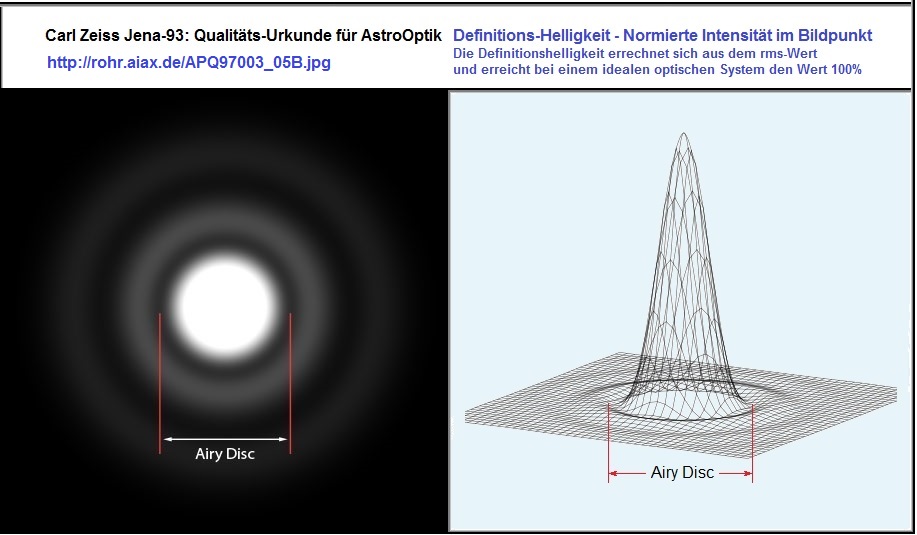
Dabei spielt der Airy-Disk Durchmesser eine Rolle, weil er bei der Strahlen-Durchstoß-Rechnung als Maßstab ver-
wendet werden kann. Zur Illustration, was der Durchmesser der Airy Disk ist, das folgende Foto. Siehe auch:
Airy-Disk Foto,___Airy-Disk: Diagramm, Airy-Disk: Formel. Ganz allgemein gilt, daß bei Obstruktion, bei Über-
oder Unterkorrektur, aber auch bei Defokussierung, ein Teil der Lichtenergie in die Beugungs-Ringe verschoben
wird. Dieses System ist also nur im Ideal-Fall eindeutig, weil eine Reihe von Einflüssen den Begriff "unscharf"
werden läßt. Passend zum Airy-Disk-Foto auch das Airy-Disk-Diagramm .

Über ein Optical Design Programm (ZEMAX) kann man nun den Strehl-Wert in Verbindung bringen zum Airy-Scheibchen, und daraus
wiederum die Auflösung ermitteln: Bei 550 nm wave wäre die Auflösung_arcsec einer Optik: 1.22*Lambda*206 265 /Apertur oder
verkürzt: Auflösung_arcsec(550 nm wave) = 138.4038 / D [Quelle: Baader, Tipps und Tricks ... ]

Der Newton-Spiegel 250/1000 f/4 hätte also 0.5536 ... Auflösung in arcsec .

Die Auflösung läßt sich aber auch über den INV Tan von (Airy Disk/2 ) / Fokus berechnen und man kommt auf den gleichen Wert:
Airy Disk = 2.44 * Lambda * Fokus / Apertur, oder verkürzt: Airy Disk (550 nm wave) = 0.001342 * Öffnungszahl. Für den Newton-
Spiegel wäre das Airy-Disk = 0.005368 mm. Geteilt durch 2 = 0.002684 mm. Dieser Wert / 1000 (Brennweite) ergibt als INV TAN

wiederum den Wert 0.55 arcsec für die Auflösung, wie bereits oben ermittelt.

Wenn aber irgend ein opt. Fehler die Abbildung beeinflusst, dann reduziert er das ideale Maximum und verschiebt darüber hinaus einen
kleinen Teil der Lichtenergie in die Beugungsringe. Das erste Bild stellt einen perfekten Newton-Spiegel dar - alles ist perfekt:
Kein Astigmatismus, keine Koma (bei Dezentrierung), keine Über-/Unterkorrektur, keine Defokussierung, keine Obstruktion etc.
.

.
Bereits ein kleiner Fokus-Shift von nur 0.018 mm reduziert den Strehlwert auf "beugungsbegrenzt", also auf einen PV-Wert von L/4 und
einen Strehl von ca. 0.80 ... und wer kann garantieren, daß er seinen perfekten Newton-Spiegel immer exakt fokussiert: Das Maximum
der Kurve wird etwas niedriger und Energie verschiebt sich in den Beugungs-Ring.

.
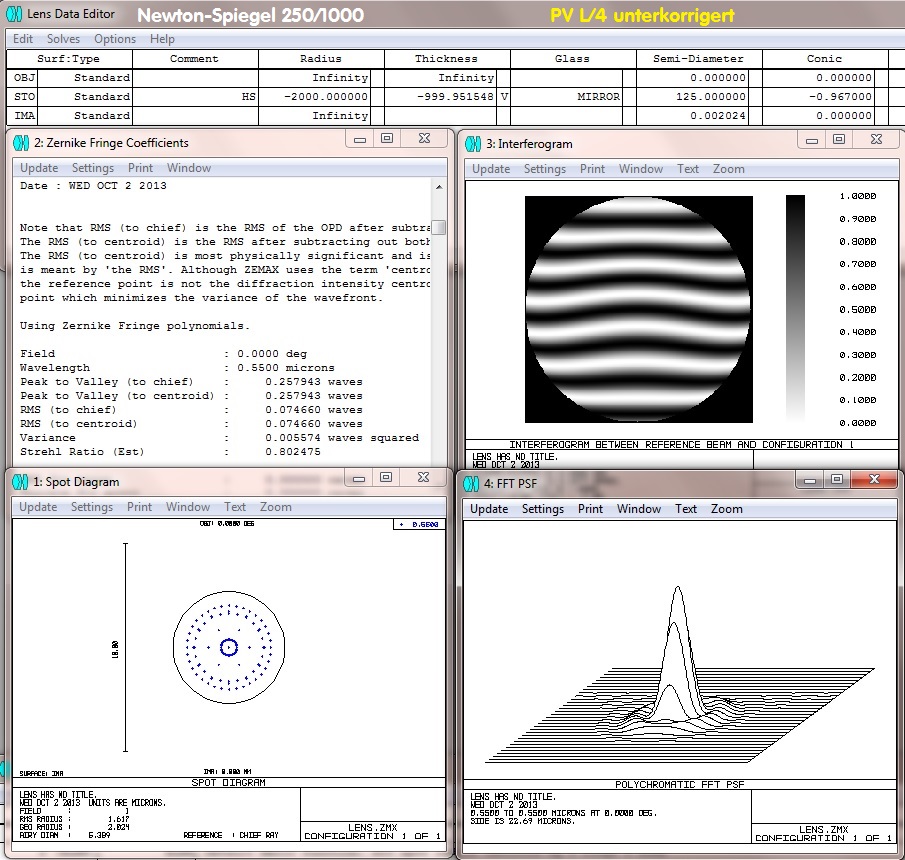
Nun haben viele Newton-Spiegel, je nach Trägermaterial, eine temperatur-abhängige Form der Oberfläche. Das kann sehr schnell PV L/3 sein.
Strehl und Temperatur - wenn sich Spiegel durchbiegen In diesem Fall reagiert die Spiegeloberfläche überkorrigiert, weshalb man
einen Newton-Spiegel immer etwas unterkorrigiert beläßt. Diese Simulation wäre also jetzt PV L/4... unterkorrigiert mit einem Strehl 0.8...
das Maximum der Kurve etwas niedriger und etwas Energie-Shift in den 1. Beugungs-Ring, aber immer noch "beugungsbegrenzt". Bei
richtiger Temperatur-Differenz zwischen Spiegel Vorder- und Rückseite, wäre dieser Spiegel perfekt, wenn alle anderen Parameter stimmen.

.
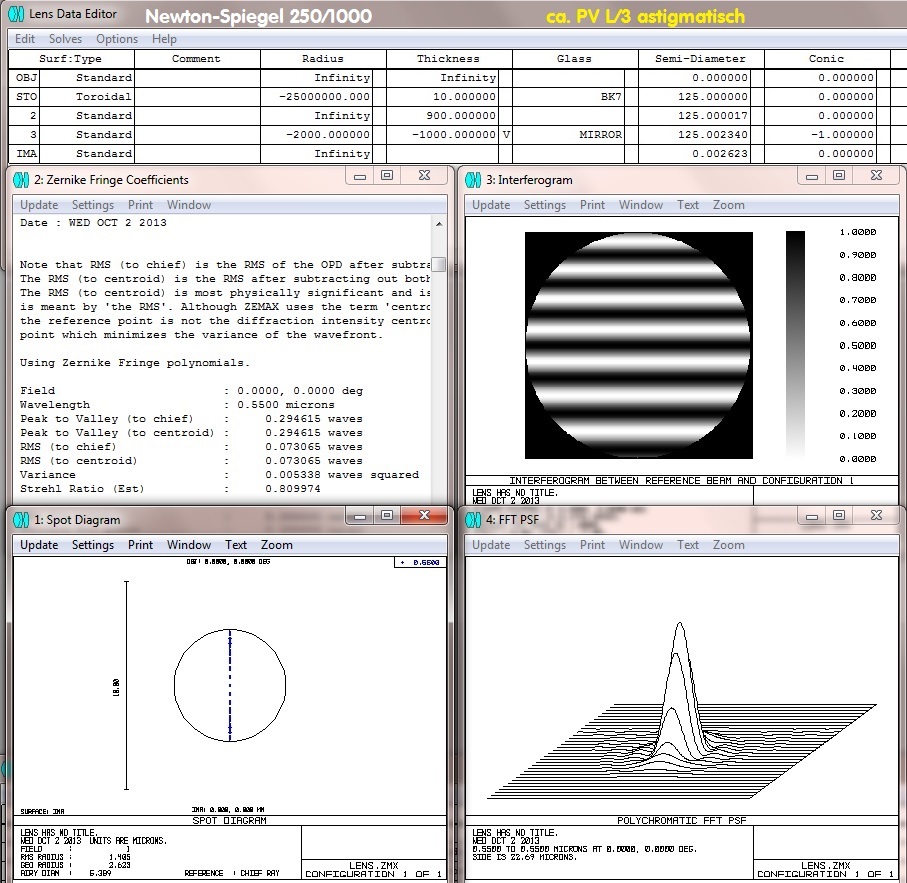
Im nächsten Beispiel hat der Spiegel einen Astigmatismus von PV L/3, egal ob vom Spiegel selbst oder von der Lagerung. Den ellipt.
Fangspiegel haben wir nicht berücksichtigt, auch der könnte eine Ursache sein. Auch jetzt wäre der Spiegel beugungsbegrenzt und
erst ab ca. PV L/3 würde man bei hohen Vergrößerung den Astigmatismus vielleicht sehen.

Soweit erst einmal die Betrachtung an einem nicht obstruierten Newton-Spiegel, der aber, wie jeder weiß, bereits durch den Fangspiegel
obstruiert wird. Je kleiner, umso besser die Abbildung - entsprechende Glätte des opt. Systems vorausgesetzt.

Was nun die Obstruktion mit der Abbildung meines künstlichen Sternhimmels an einem Kugelspiegel macht, sieht man auf dem nächsten Bild:
Der Kugelspiegel hat 250 mm Durchmesser bei 2400 Radius. Die Auflösung des künstl. Sternhimmels, auf dem Foto unten links liegt bei etwas 0.006.
Geteilt durch den Radius von 2400 mm ergibt das 0.52 arcsec und liegt damit ebenfalls im Bereich des oberen 250 mm Newton-Spiegels.

Nun käme aber die Obstruktion von a) 100 mm und b) 166 mm hinzu, und man beobachtet eine kräftige Energie-Verschiebung in die BeugungsRinge,
was den Sternscheibchen Durchmesser kräftig aufbläst. Das geht genaugenommen wiederum auf Kosten des Strehlwertes, an dem sich aber bei der
Auswertung erst einmal nichts ändert.
Strehlwert und Obstruktion - Modulationsübertragungsfunktion

Für die Praxis heißt das, daß der Strehl-Wert nicht das alleinige Kriterium für opt. Qualität sein kann, bei Spiegeln wäre z.B. auch die Glätte ein wichtiger Aspekt.
Bei der Astro-Fotografie liefert selbst ein überkorrigiertes GSO RC-System hervorragende Ergebnisse ab, weil die Abbildung im Bildfeld das eigentliche
Kriterium ist. Da interessiert sich kaum einer für den Strehlwert auf der opt. Achse.