F064 Radius-Vermessen mit Endmaßstäben aus Silberstahl
Die Gemeinheit des Messen
Nicht umsonst gibt es den Beruf des Meßtechnikers, weil es sehr viele Klippen sind, bis man sich einigermaßen
sicher sein kann, daß das Ergebnis auch stimmt. In vorliegendem Fall geht es lediglich darum, den Krümmungs
Radius einer Parabel auf der Achse messen zu wollen. Und obwohl es sich "n u r" (!!!) um eine Längenmessung
handelt, ist man mit einer Reihe höchst interessanter Probleme konfrontiert:
Das Problem beginnt damit, daß man lange suchen muß, ob man eine Firma findet, die Längenmaße über 500 mm auf 0.01
mm genau messen kann. Bis 500 mm stehen mir selbst 3 Meßschieber zur Verfügung: ein 150 mm, ein 300 mm und schließ
lich noch ein 500 mm mit einer Genauigkeit in der Gegend von 0.01 mm auf der gesamten Meßstrecke. Die waren auch
nicht gerade billig. Und im Zusammenhang mit meiner großen Drehbank hatte ich mir auch noch einen 800 mm Meßschie-
ber zugelegt aus Fernost, und mit dem erlebte ich zunächst erst einmal meine blauen Wunder.
Also besorgte ich mir Rundstäbe aus Stahl, Automaten-Stäbe genannt mit Durchmesser 6 mm, längte sie mit einem Auf-
maß in der Gegend von 2 mm ab, und vermaß sie bis zu 500 mm mit den drei Meßschiebern so genau, wie es ging, bei
einer Raumtemperatur von 22° Celsius. Die Stirnseite der Stäbe schliff ich mit einer 32 000 U/min laufenden Drehspindel
auf eine saubere Fläche in meiner Drehbank. Die bis zu 500 mm langen Stäbe wurden also ziemlich genau. Wie genau,
kann man der folgenden Tafel entnehmen.
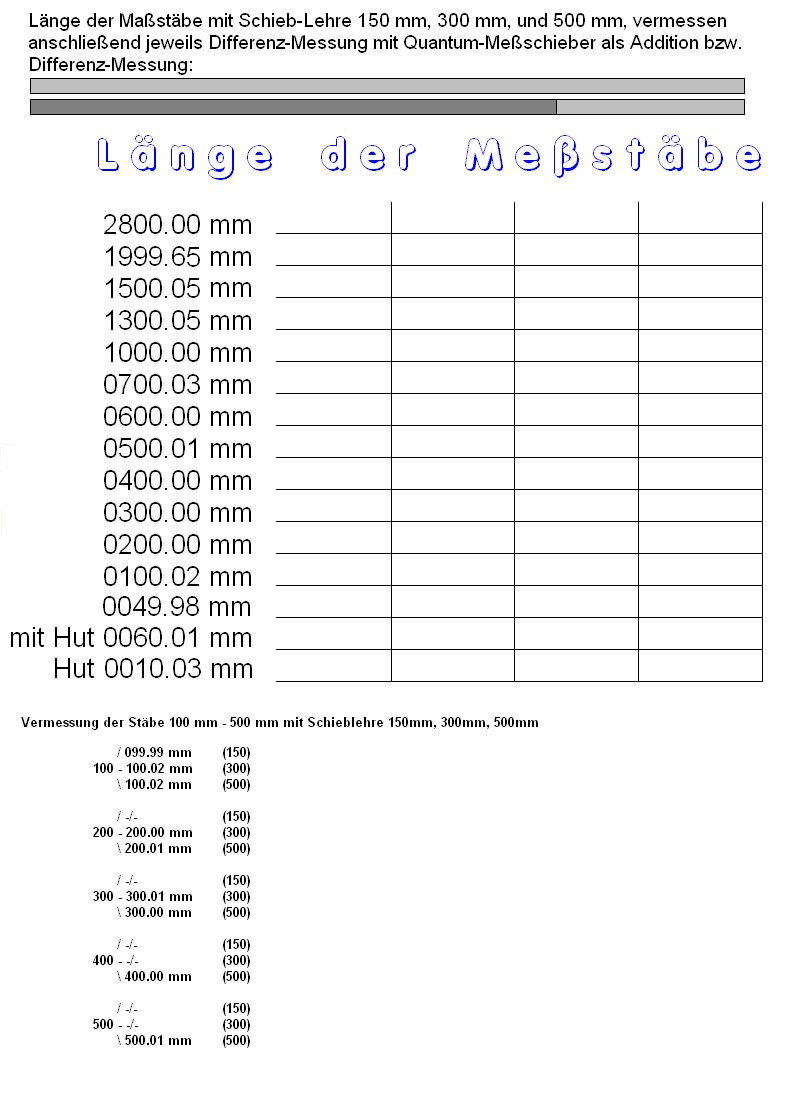
Wie selbst genaue Meßschieber noch differieren können, erkennt man an folgenden Bild, wobei der 150 mm Meßschieber täglich in Gebrauch ist, und dadurch ein Abnutz-Effekt eine Rolle spielen könnte.

Bis 500 mm gestaltet sich die Längenmessung einigermaßen zuverlässig bei einer geschätzen Genauigkeit von 0.01 mm.
Man sieht auch das Sortiment meiner End-Maß-Stäbe: 100, 200, 300, 400, 500, 600, 700, 1000, 1300, 1500, 2000, 2800 mm

Nun geht es um die Mitte der Bikonvex-Linse, die man mit der Schieblehre herausmessen kann und mit einer dünnen Linie
anreißt.

Derart vorbereitet geht man in den Krümmungsmittelpunkt eines Newton-Spiegels und erzeugt mit dem Bath-Interfero-
meter das folgende Interferogramm. Da man den Radius auf der Achse messen will, also im Zentrum des Spiegels selbst,
müssen dort die Streifen gerade und parallel sein. Man könnte den Spiegel auch auf einen kleinen Durchmesser ab-
blenden, und dann würde er in der Mitte die Bedingungen einer Sphäre erfüllen. Da nun beim Bath-Interferometer diese
kleine Bikonvex-Linse doppelt benutzt wird, a) für das Inforamtions-Bündel und b) für das Referenz- oder Vergleichs-
Bündel, muß der Punkt, von dem aus man zum Spiegel mißt, exakt in der Mitte dieser kleinen Linse liegen, wenn die
Interferenz-Streifen parallel und gerade sind, wie bei einer Sphäre.

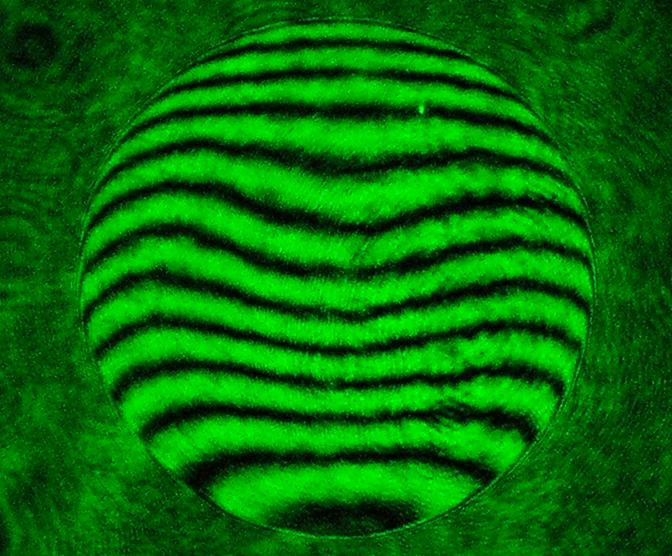
Nach diesem Verfahren könnte man mit einem Bath-Interferometer auch Zonen-Messungen veranstalten. Man müßte nur
darauf achten, daß in der jeweiligen Zone die Streifen gerade und parallel sind, wie das nächste Bild zeigt. Hier würde
man etwa in der 70.7% Zone messen. Das Foucault-Verfahren oder die Caustik-Methode ist aber in diesem Fall genauer.
Auf der anderen Seite muß man nun die Spiegeloberfläche berühren, ohne sich Kratzer einzuhandeln. Ein Kunstostoff-Stift
erledigt die Sache, sodaß man nun durch Addition der Endmaß-Stäbe den vorher mit dem Interferometer eingestellten
Radius ausmessen kann.

Das schaut dann so aus, wobei der Rest mit einer Schieblehre ermittelt werden muß.

Und die zeigt dann dieses Ergebnis. Einschränkend muß man aber dazu sagen, daß der "Eichstrich" zugleich der kritische
Punkt ist: Sollte man am besten unter einem Mikroskop erledigen, damit es auf 0.1 mm stimmt. Über die Addition der
Endmaßstäbe bekommt man im konkreten ca. Fall 2364 mm, ein Wert der bei bester Genauigkeit in der Gegend von 0.1
mm Toleranz anzusiedeln ist durch die Addition aller möglichen Einflüsse.

Mit dem Metallband ergibt sich etwa ein Betrag von 2365.2 mm, wobei einmal das vordere Ende genauer unter die Lupe
genommen werden müßte und ebenso die Mißweisung auf einer Strecke von 2365 mm. Bei allen Vergleichsmessungen
ergab sich eine Differenz von ca. 1 mm bei einer Meßstrecke von 2000 mm. Davon ganz unberührt, ist bei der ROC Aus-
wertung der exakte Rand es Interferogrammes vermutlich schwerer zu bestimmen.
Eine andere Form der RoC-Auswertung geht mit dem Foucault-Test, also die zweite Variante, den Krümmungsradius zu
bestimmen. Aber das ist der zweite Beitrag, der noch kommt.

#########################################################################################################
Hallo Detlev,
für die Diskussion eine uferlose Angelegenheit!
Aaaaaaaaaaaaber, die wichtigste Frage bleibt weiterhin, wie groß muß denn überhaupt die Genauigkeit sein? Bezogen auf den Krümmungsradius reicht eine Genauigkeit von +/- 1 mm, und die ist mit diesem Verfahren möglich.
Die Gegenkontrolle über Foucault, wobei der 200 mm Newtonspiegel auf 50 mm abgeblendet wurde: Auch hier ergibt sich ein Ergebnis mit einer Genauigkeit von 0.1 mm zum oberen Ergebnis. Aber auch hier kann man die Differenz zwischen Endmaß und Metallbandmaß von ca. 1 mm erkennen. Bei sorgfältiger Vorgehensweise sollte also tatsächlich eine Genauigkeit von mindestens 0.2 mm erzielbar sein, schon deswegen, weil der Foucault-Test im Bereich von 0.01 mm mißt.

Übrigens: http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/10/waermetransport/waermedehnung/waermedehnung.vlu/Page/vsc/de/ch/10/waermetransport/waermedehnung/laengenausdehnungskoeffizient/laengenausdehnungskoeffizient.vscml.html
Quote:
Tab.3lineare Längenausdehnungskoeffizient von festen Stoffen Temperaturbereich 0 °C - 100 °C 0 °C - 200 °C Aluminium 23,8 24,5 Gusseisen 10,4 11,1 Kupfer 16,5 16,9 Messing 18,4 19,2 Stahl (unlegiert) 11,0 12,2 Quarzglas 0,50 0,59
Oft wird auf die exakte Ermittlung vonin einem Temperaturbereich von
bis
verzichtet und bei Berechnungen näherungsweise der Wert für den Temperaturbereich von
bis 0 °C eingesetzt.
Bei einem Grad Temperatur-Differenz bringe ich für die Länge von 2400 mm eine Längendifferenz von 0.026 mm heraus.
Das wäre ja wirklich zu verkraften.
Fortsetzung
... Unterzieht man meinen Eichstrich auf dem Interferometer einer kritischen Prüfung, dann muß er um ca. 0.7 mm nach
links justiert werden. Also das Ganze noch einmal:Weil gerade Foucault aufgebaut war, der auf 50 mm abgeblendete 200
f/6 Newton.

Foucault/Endmaß ein Wert von 2 364.36 mm; das Endmaß stößt links an die Klinge an.

Foucault/Bandmaß ein Wert von 2 365.6 und somit eine Differenz Endmaß/Bandmaß + 1.2 mm

Interferometer/Endmaß Gesamtergebnis: 2 364.76


Interferometer/Bandmaß Ergebnis 2366.00 mm und somit eine Differenz Endmaß/Bandmaß + 1.2 mm

Die Differenz Foucault / Interferometer wäre bei ca. 0.4 mm, also immer noch weit unter der sinnvollen Toleranz von
1 mm, ein Wert der auch für einen Zygo genügen würde.Damit sollte Stoffies Frage, wie man mit einem
Bath-Interferometer den Krümmungsradius einer Parabel ausmißt, hinreichend dargestellt sein. Es ist schon
ein gewisser Aufwand vonnöten ...
################################################################################################################
Hallo Donald,
Selbst in der 70.71% Zone wenn Du mißt dann wäre die Abweichung immer noch gering nach der Formel (H^2/2*R)/2 bei
bewegter Lichtquelle, wie das bei mir der Fall ist. Im Falle des 200/1183 Parabolspiegels wäre das gerade mal 1 mm, den
Du zuviel gemessen hast. Die weißen Linien zeigen, wo die Streifen parallel und gerade sein müssen.

