elliptical Flats ___________________ siehe auch: Fangspiegel-Qualität bei einem Newton und Elliptische Flats / Planspiegel testen
__
Es geht um die Frage, welche Genauigkeit bei einem Newton-System der elliptische Flat haben muß bzw. haben soll, und der Frage, wie man das
eventuell merken könnte. Die Prüfung auf der opt. Bank erfolgt so, wie dieser 70 mm Flat in das spätere System eingebaut wird, also im 45° Winkel
zur opt. Achse des Hauptspiegels. Geprüft wird gegen einen dafür hinreichend genauen (PV L/10 der Wellenfront) 150 R 600 Kugelspiegel, sodaß
der Flat selbst im Doppelpaß geprüft wird. Bei Edmund Scientific bekommt man derartige Kugelspiegel.

Wichtige Vorbemerkung:

Je nach Positionierung des Newton-Fangspiegels wird in der Regel nur ein Teil der opt. Plan-Fläche benutzt. Bei diesem Test wird aber die gesamte
Planfläche vermessen, sodaß der ellipt. Planspiegel opt. umso besser ist, je kleiner die im Strahlengang benutzte Fläche tatsächlich ist.

A: erforderliche Genauigkeit der Referenz-Sphäre

Der Durchmesser von 150 mm dürfte ausreichend sein für Flat-Durchmesser bis max. 100 mm kleine Achse, im äußersten Fall stünde ein 250 mm Kugelspiegel
ebenfalls zur Verfügung.

Zunächst wird man sich meßtechnisch mit dem Kugelspiegel selbst befassen: Wie wird der Artificial Sky Test über den Kugelspiegel im einfachen Durchgang abgebildet.
Damit ist u.a. eindeutig, daß kein signifikanter Astigmatismus eine Rolle spielt für den Gesamt-Durchmesser 150 mm. Als Auflösung ergeben sich die angegebenen
Werte, die sowohl über die Formel und das Foto ermittelt werden können.

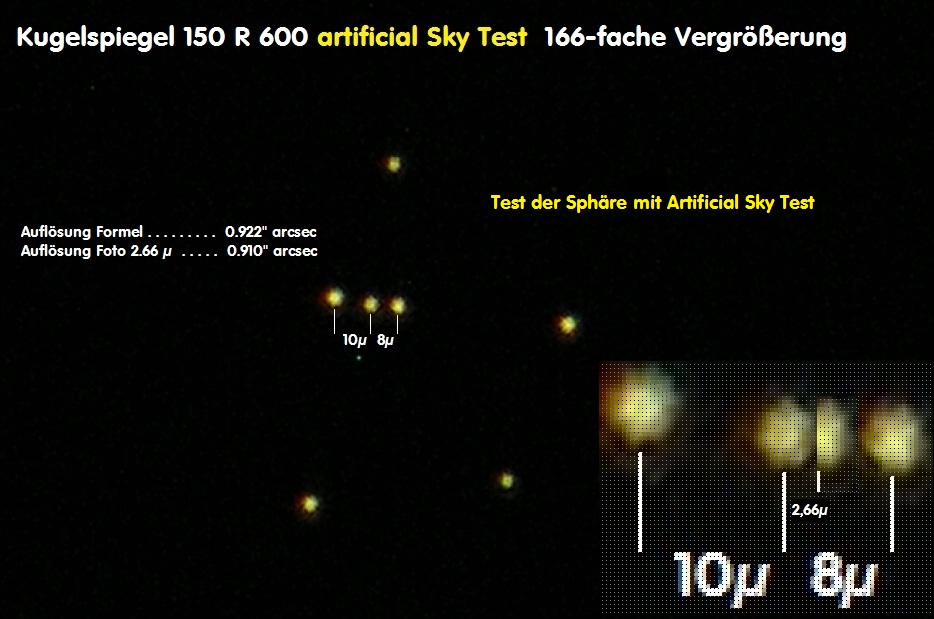
Bei diesem f/4 Lichtkegel spielt es eine wichtige Rolle, daß dieser Test exakt auf der opt. Achse erfolgt, da sich sonst Astigmatismus "einschleichen"
würde. Dies erforderte einen Umbau der ursprünglichen Art Sky Version.

Der Kugelspiegel wird bei diesem Test nur mit dem Durchmesser des elliptical Flats benutzt, also mit 70 mm kleine Achse. Entsprechend genau ist für diesen Fall
der Kugelspiegel als Referenz-Spiegel in der Gegend von mindestens PV L/10 der Wellenfront.

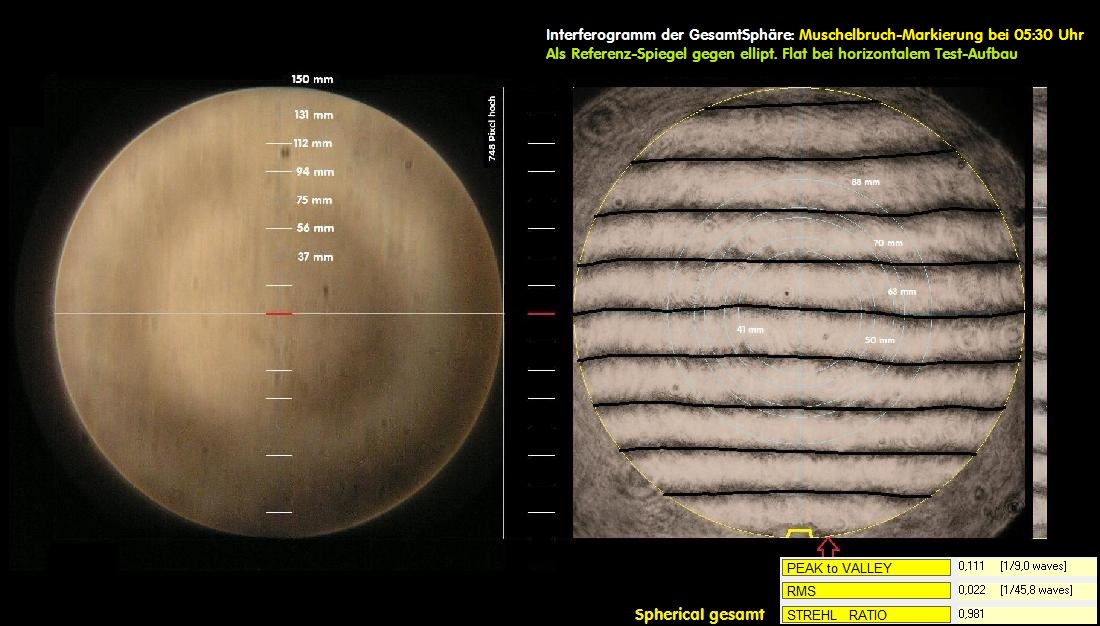
Das für den Durchmesser 70 mm maßgebliche Interferogramm . . .

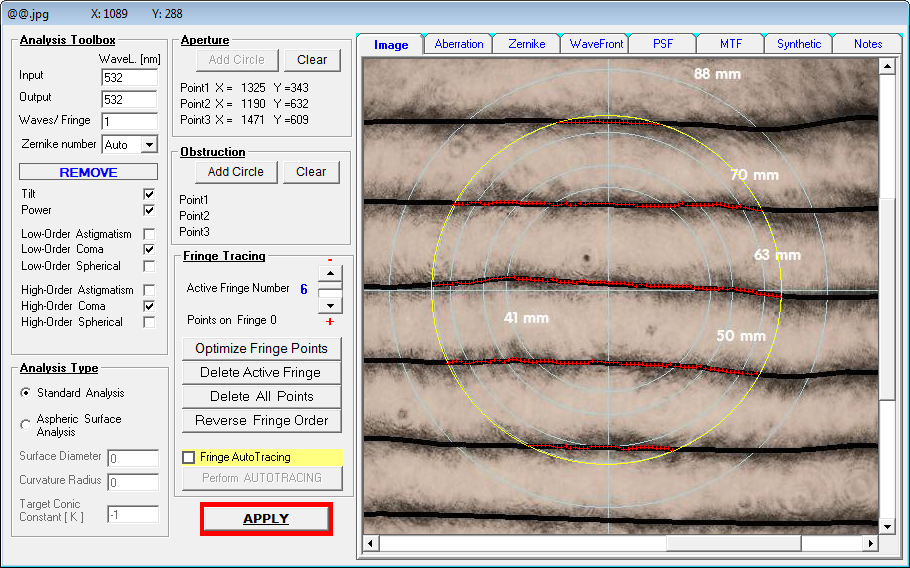
Die Wellenfront-Deformation . . .

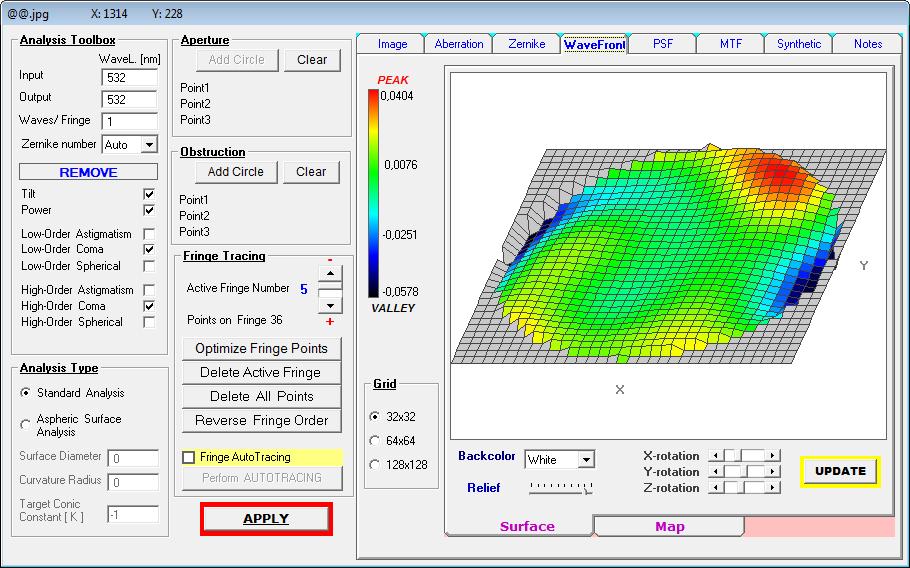
und schließlich das PV-Ergebnis der benötigten Referenz-Fläche von PV L/10 der Wellenfront oder PV L/20 der Oberfläche.

B: ein Beispiel mit PV L/4 der Wellenfront bzw. L/8 der Oberfläche

Im nächsten Schritt ein elliptischer Planspiegel, wie er in jedem Fall funktioniert indem er eine gute Abbildung abliefert in der möglichen Auflösung.

Wer die Testbilder vom Kugelspiegel mit dem 70 mm Flat vergleicht, dem wird auffallen, daß das Bild des sphärischen Spiegels deutlicher ausfällt. Das hat mit dem
Durchmesser/Radius-Verhältnis zu tun, die in den beiden Fällen unterschiedlich ist: Kugelspiegel [150 R 600], Flat [70 R 600]. Für den Durchmesser 150 mm
errechnet sich also eine höhere Auflösung als für den Durchmesser 70 mm, wobei das nur für die Kugel bzw. den aktuellen Flat gilt, nicht, wenn er im System
eingebaut ist.

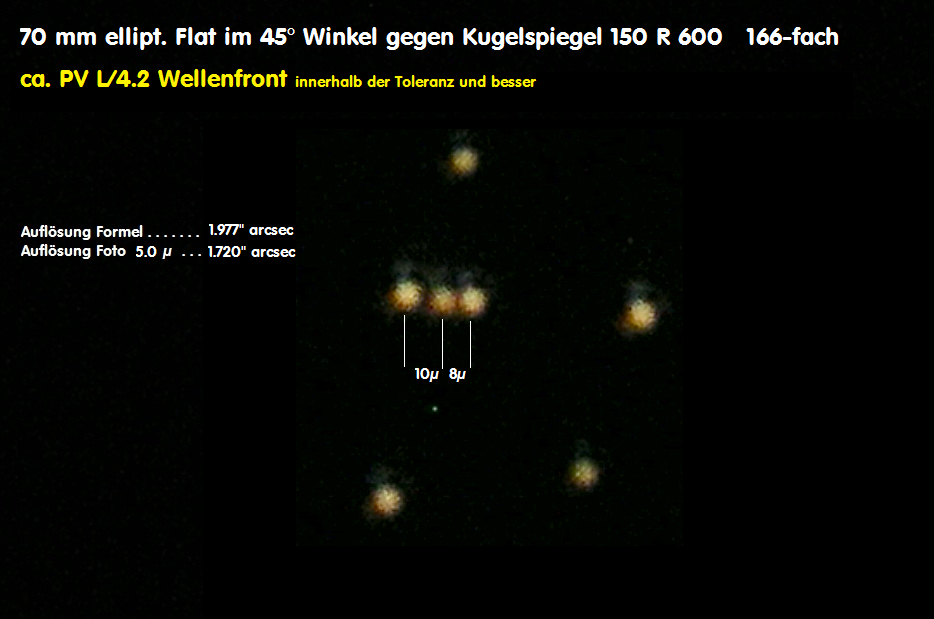
Immerhin hat also dieser ellipt. Planspiegel die erforderliche Genauigkeit von PV L/4 der Wellenfront und besser oder PV L/8 der Oberfläche und besser.

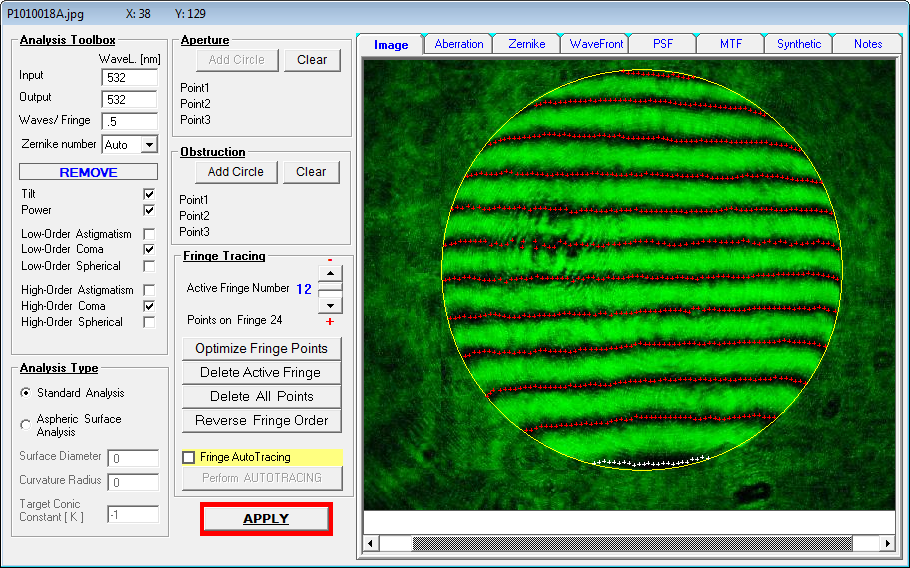
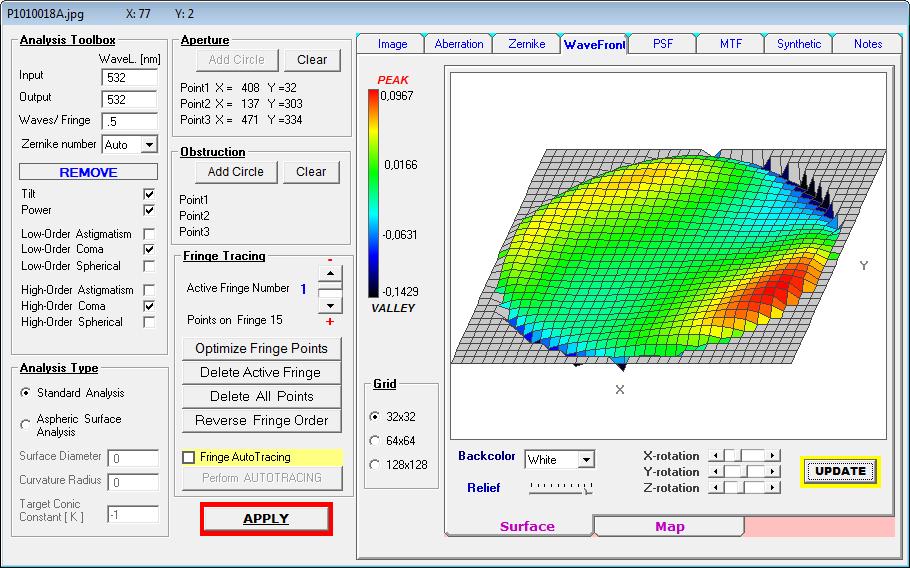
Man wird diesen Flat unbedingt empfehlen können.

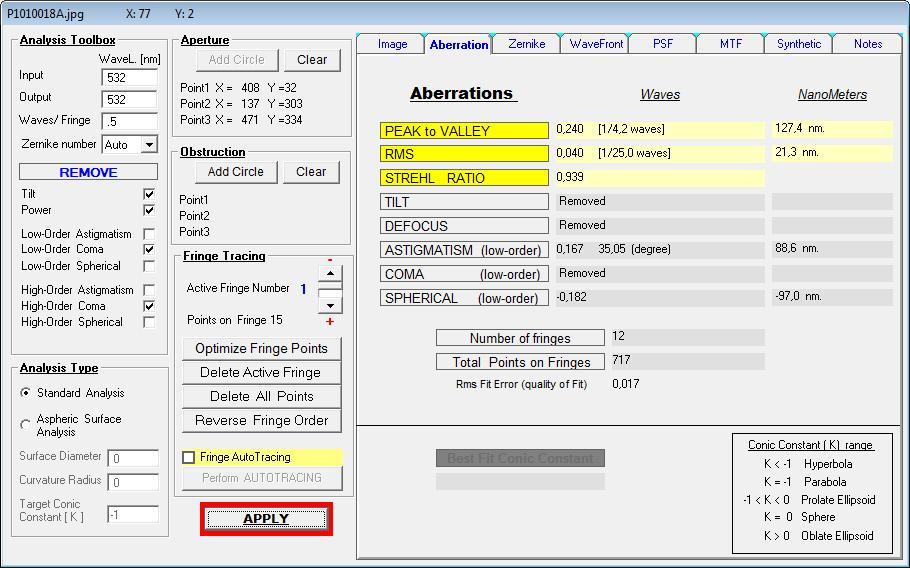
C: ein Beispiel mit PV L/1.4 der Wellenfront bzw. L/2.8 der Oberfläche,

Dazu zunächst die Vorbemerkung von ganz oben:
Je nach Positionierung des Newton-Fangspiegels wird in der Regel nur ein Teil der opt. Plan-Fläche benutzt. Bei diesem Test wird aber die gesamte Planfläche
vermessen, sodaß der ellipt. Planspiegel opt. umso besser ist, je kleiner die im Strahlengang benutzte Fläche tatsächlich ist. Das Meßergebnis bezieht sich bei
diesem Beispiel auf den Gesamt-Durchmesser/kleine Achse des elliptischen Planspiegels.

Das zweite Beispiel lädt zu aus-ufernden Diskussionen ein. Ein versierter Beobachter würde bei hoher Vergrößerung schon merken, daß das opt. System Newton
nicht ganz in Ordnung ist. Die Frage aber stellt sich, wie brauchbar ist die Abbildung mit diesem eindeutigen schlechteren Planspiegel?

Den ersten Hinweis liefert wieder der Artificial Sky test. Der Astigmatismus reduziert im Fokus die Abbildung con ca. 1 Bogensekunde auf ca. 3 Bodensekunde.
Das Seeing ist in unseren Breiten ebenfalls nicht immer perfekt und nun kann man mutmaßen, welcher der Gründe den Ausschlag gibt. Bei niedrigen Vergrößerungen
wird man davon erst einmal gar nichts sehen. Das wäre also ein qualitativer Test bei optimalem Seeing auf der opt. Bank. Der Astigmatismus kann auch damit zu
tun haben, daß auf dem Planspiegel ein Radius liegt und bei einem Winkel von 45° als Astigmatismus-Effekt zu sehen ist. Das hätte dann mit der Planität bzw. der
Power zu tun.

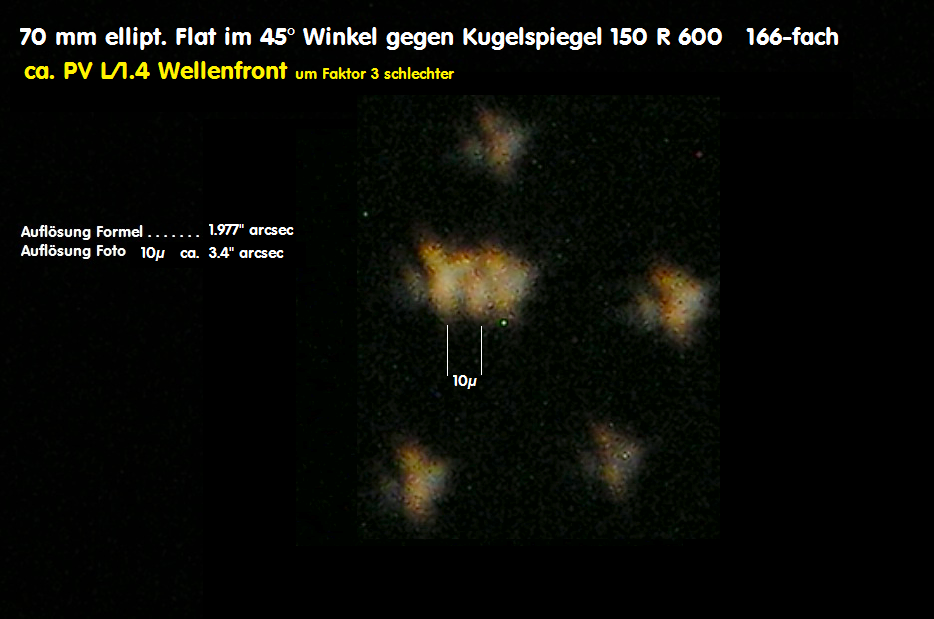
Dem Interferogramm sieht man den Astigmatismus deutlich an - etwa in der Nähe von 1* Lambda PV der Wellenfront.

Ob nun die Power/Planität den Ausschlag gibt, müßte nun über die Kontakt-Probe gegen einen Referenz-Flat ermittelt werden. Die Wellenfront
Darstellung spricht dafür, daß die Power nicht ganz stimmt.

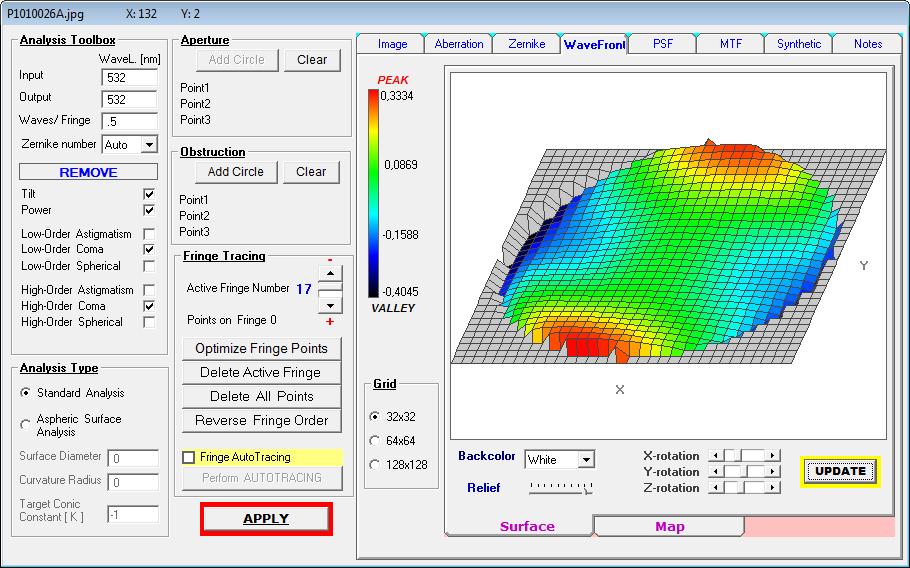
Dieser 70 mm Flat wird also bei hohen Vergrößerungen "einbrechen", so der Hauptspiegel keine weiteren Fehler einführt und das System
exakt zentriert ist - und natürlich das Seeing einen kritischen Blick erlaubt.

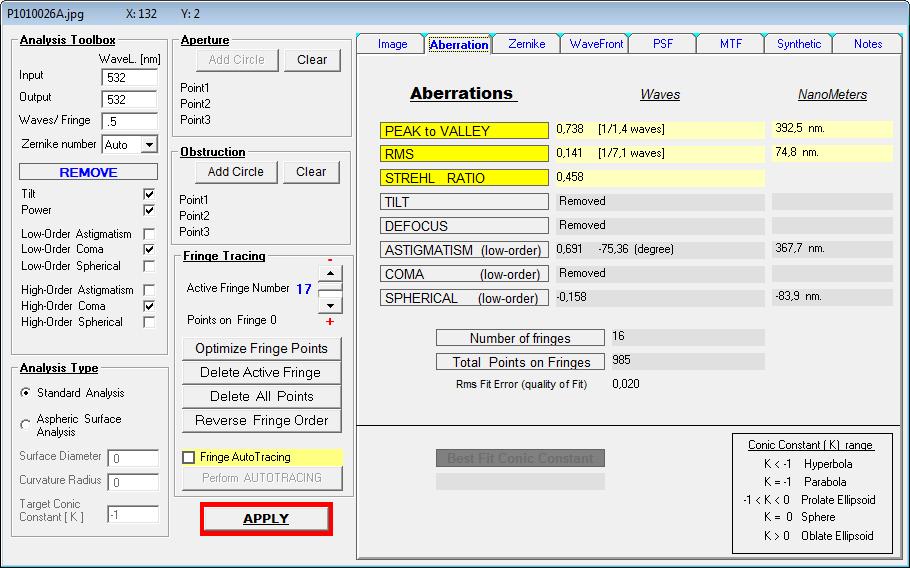
Damit ist aber die Frage nach der durchschnittlichen Qualität von elliptischen Planspiegeln überhaupt nicht beantwortet, und das würde mich
am allermeisten interessieren, mit welcher Qualität man es dann zu tun hat.

#####################################################################################################

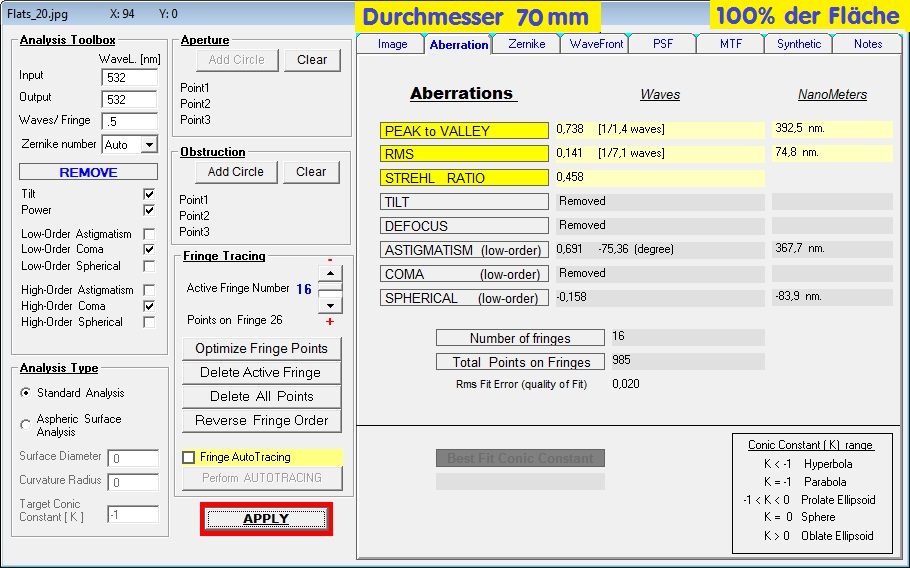
Je kleiner der Durchmesser, umso genauer die benutzte Fläche bei ein und demselben ellipt. Fangspiegel.

 

#####################################################################################################

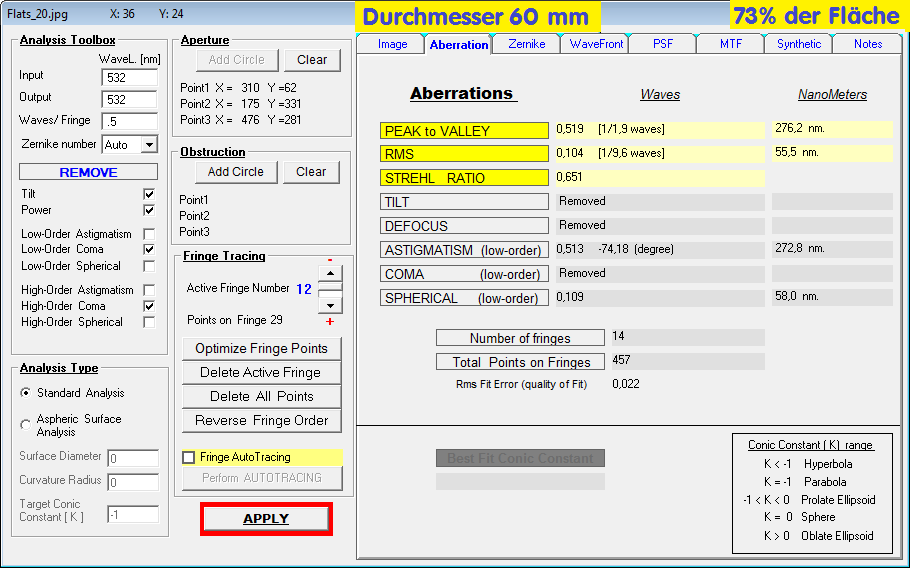
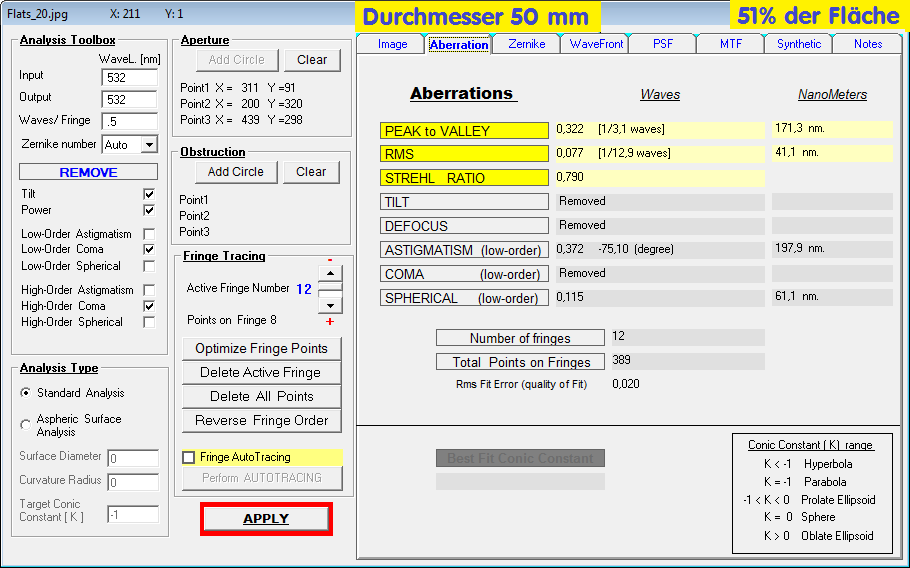
Es stellt sich noch die Frage, ob der oberste Test-Aufbau mit doppelter Genauigkeit viel zu kritisch sei, und bei einfacher Genauigkeit wäre der Astigmatismus nicht so gravierend zu erkennen. Dieser Einwand taucht prinzipiell beim Sterntest auf und bezieht sich auf den farbigen Farbsaum. In diesem Fall geht es um die Darstellung eines astigmatischen Fangspiegels = elliptical Flat. [url='http://www.astro-foren.de/showthread.php?p=42829#post42829'][b][color=#417394]Test im einfachen Durchgang mit einem Newton-Spiegel[/color][/b][/url] Der obere Link zeigt einen Testaufbau im einfachen Durchgang. Wenn ein ellipt. Planspiegel geprüft werden soll, braucht man lediglich ein gutes APO-Objektiv, hinter dem der Fangspiegel den Strahlengang um 90° abwinkelt. Damit kann die Genauigkeit des Fangspiegels über den Artificial Sky Test im einfachen Durchgang gezeigt werden und führt zu gut unterscheidbaren Ergebnissen. (Will man hingegen ein Interferogramm erzeugen, dann geht man entweder in den doppelten Durchgang zurück, oder bemüht den [b][url='http://www.astro-foren.de/showthread.php?8046-Point-Diffraction-Interferometer&p=31244#post31244']Point Diffraction Interferometer[/url].[/b] (Es muß dann lediglich der Streifenabstand berücksichtig werden.) Während abhängig vom Fangspiegeldurchmesser im Idealfall die Auflösung bei ca. 2" arcsec liegt, [b]bezogen auf den Fangspiegeldurchmesser 63 mm im Testaufbau[/b]. Bei einem fehlerhaften Fangspiegel dürfte sich deshalb die Auf- lösung auf ca. 4" arcsec reduzieren, [b]wieder bezogen auf den Testaufbau und den Durchmesser 63 mm, über den die Artificial Sky Testbilder entstanden sind[/b]. Es ist ein qualitativer Test bei dem die Auflösung u.a. über die Formel berechnet wird: Auflös.= 1.22*Lambda*206265/Öffnung oder 138.4038/Öffnung [für Lambda = 550 nm wave] oder über das jeweilige Foto mit inv TAN(Abstand/Fokus) Beispiel INV TAN(0.01/800). [size=14][color=#ff0000][b]@ [/b][/color][/size][url='http://www.astro-foren.de/showthread.php?t=7874'][b]Artificial Sky[/b][/url][b] : Prinzip[/b] [img]http://rohr.aiax.de/Flats_25.png[/img] [b][size=12]Das Prinzip [/size][/b][img]http://rohr.aiax.de/Flats_29.png[/img] [b][size=12] ein Parallel Bündel wird erzeugt[/size][/b] [img]http://rohr.aiax.de/Flats_30.jpg[/img] [b][size=12]geprüft wird der elliptische Planspiegel - siehe die oberen Testbilder[/size][/b] [img]http://rohr.aiax.de/Flats_31.jpg[/img] --------------------------------------------------------------------------

Zum Thema gibt es von Philipp Keller einen älteren Interstellarum-Bericht von 4/95, der die Thematik mit ZEMAX simuliert. Damit lassen sich jeweils nur
typisierte Fehler darstellen. Prinzipiell erzeugt ein flacher Radius auf dem Flat Astigmatismus, der Strehl-mindernd wirkt und damit die Auflösung drückt,
siehe das zweite Bild. Mit dem Artificial Sky Test läßt sich zum Strehlwert ebenso die reduzierte Auflösung darstellen, wobei auf unterem Beispiel-Fotos
eine hohe Vergrößerung von 666-fach berücksichtigt werden muß, sodaß bei niedriger Vergrößerung die Fehler schwerer zu entdecken sind.

Wenn ein flacher Radius auf dem Fangspiegel liegt, dann entsteht zwar Astigmatismus, der sich im System selbst nicht verändert. Anders ist die Situation,
wenn der Fang- oder Planspiegel-Spiegel statt einem "flachen Radius" eine torische Fläche darstellt. Je nach Lage stört der Astigmatismus weniger, wenn
er längst zum Strahlengang steht, und stärker, wenn er quer dazu liegt oder diagonal. Auch läßt sich ein möglicher Astigmatismus auf dem Hauptspiegel
durch Verdrehen gegen den Fangspiegel kompensieren. Ein kleiner Astigmatismus-Wert auf dem Hauptspiegel läßt sich gegen die Koma beim Newton-
System ausspielen, zumindest für visuelle Anwendungen.

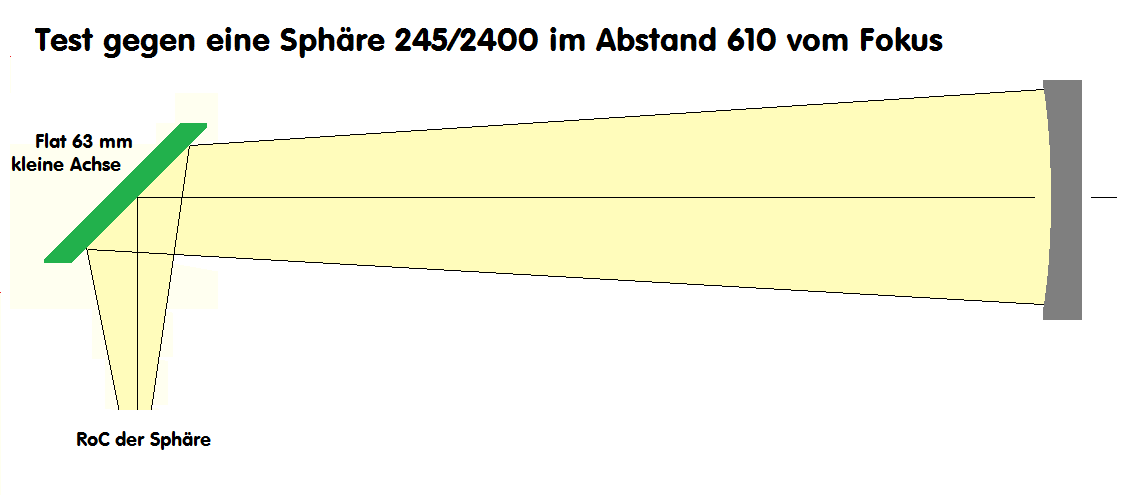
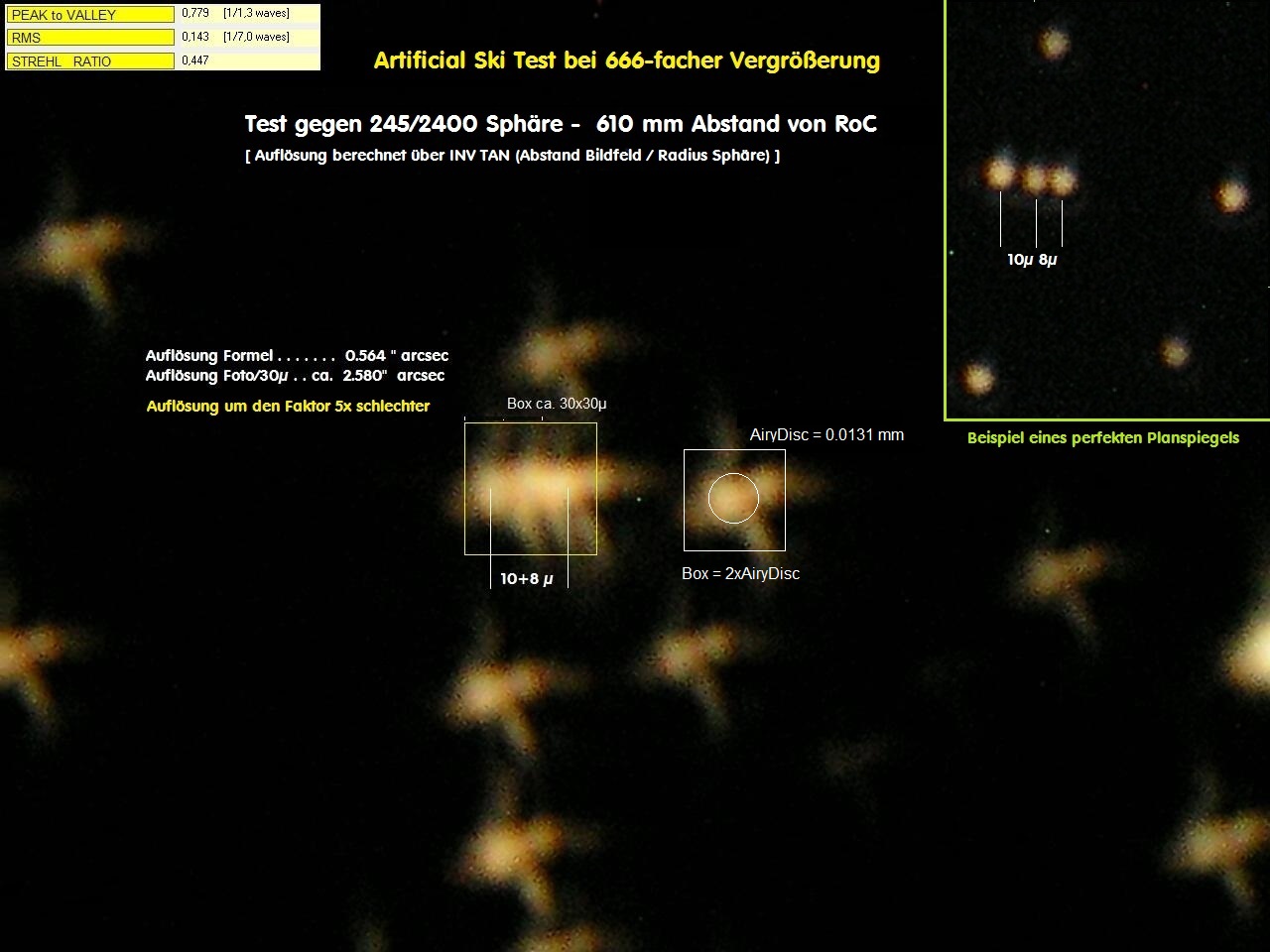
Je nach Testaufbau und Größe der Vergleichs-Box reduziert sich die Auflösung um das 3-5-fache des Ideal-Wertes bzw. der theoretischen Auflösung.
Da in der Regel die Vergrößerungen sehr viel niedriger sind, wird man den Astigmatismus eher weniger bemerken. Es stellt sich immer wieder die
Frage, welche Genauigkeit brauchen diese elliptisc hen Flats. Für anspruchsvolle Beobachter sollten es ca. PV L/4 der Wellenfront bzw. PV L/8 der
Oberfläche sein. Bei niedrigen Vergrößerungen wird man auch bei der Hälfte dieser Werte noch keine Qualitäts-Einbußen feststellen, was letztlich
auch eine Frage des Preises ist. Das Bild entstand beim Test eines 63 mm kleine Achse Flats gegen einen 245/2400 Kugelspiegel im Abstand 610 mm
vom Krümmungsmittelpunkt. Dort wird der Fangspiegel ganz ausgeleuchtet bzw. gemessen.

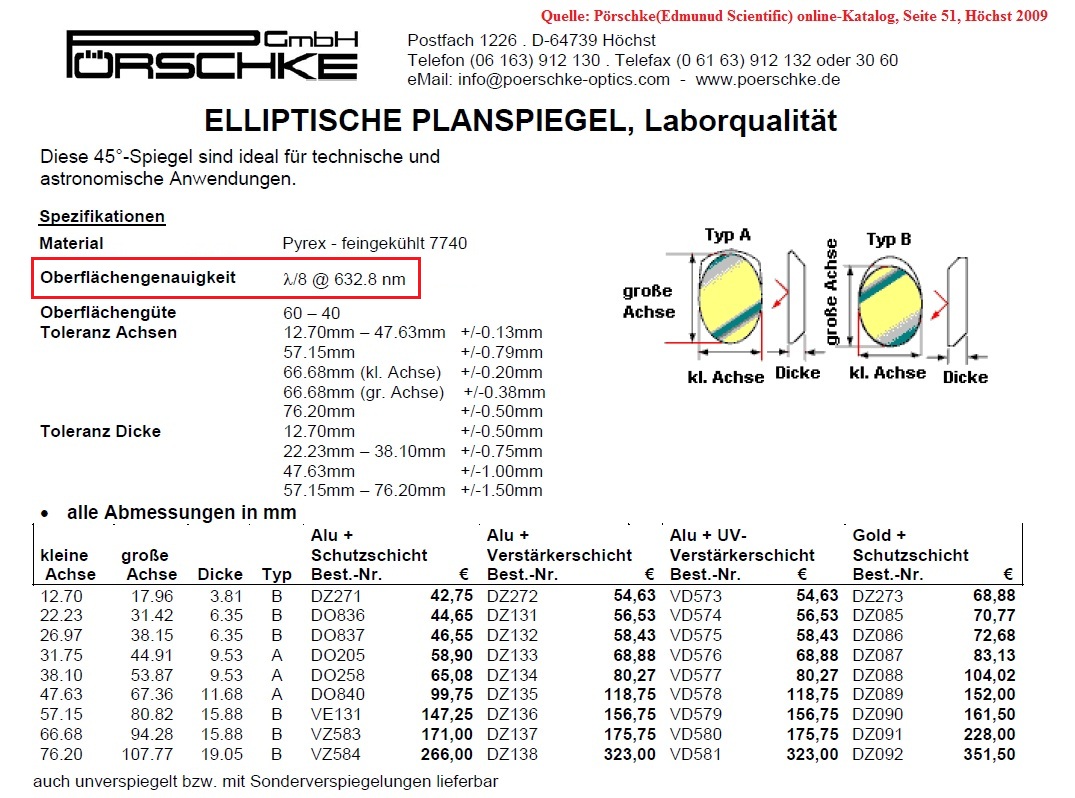
Ein Anhaltspunkt sind auch die bei Edmund Scientific/Pörschke angegebenen Toleranz-Werte von PV L/8 der Oberfläche bzw. PV L/4 der Wellenfront. Man kann also davon
ausgehen, daß diese Genauigkeit im Allgemeinen ausreichend ist.

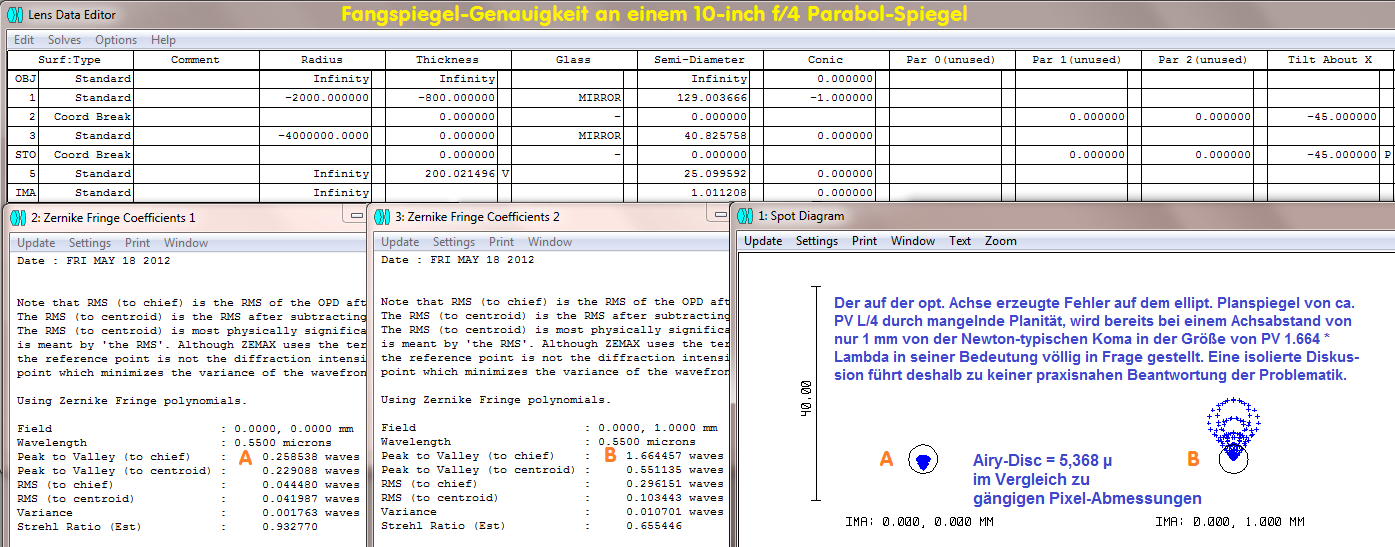
Geradezu konterkarriert wird eine isolierte Genauigkeits-Diskussion beim ellipt. Fangspiegel, wenn man die bei einem Newton-Teleskop systembedingte
Koma außerhalb der opt. Achse ins Spiel bringt: Bereits bei einem Achsabstand von nur 1 mm, der über eine fehlerhafte Justierung fast immer vorkommt,
übertrifft der Komafehler des Systems Newton den Fangspiegel-verursachenden Fehler um den Faktor 6 bezogen auf einen der üblichen f/4 Newtons.
Während Rest-Astigmatismus im Fokus zu einem kleinen Kreuz abgebildet wird, erkennt man die Koma sehr viel schneller über die typische "Kometen"-
Form und fällt besonders bei der Fotografie in den Bildecken auf oder im Randbereich von Okularen, wenn man nicht gerade einen Koma-Korrektor benutzt.

 

##################################################################################

Gewichtung: Fangspiegel-Fehler gegen leichte Dezentrierung beim Newton

Ausgehend von einem fehlerfreien f/4 Newton-System 250/1000 ist dieses System nur dann fehlerfrei, wenn die Zentrierung perfekt ist. Bereits ein
Achsabstand von 1 mm - wie er häufig bei fehlerhafter Zentrierung vorkommt - verursacht mehr Fehler, als vom Fangspiegel eingeführt werden kann.

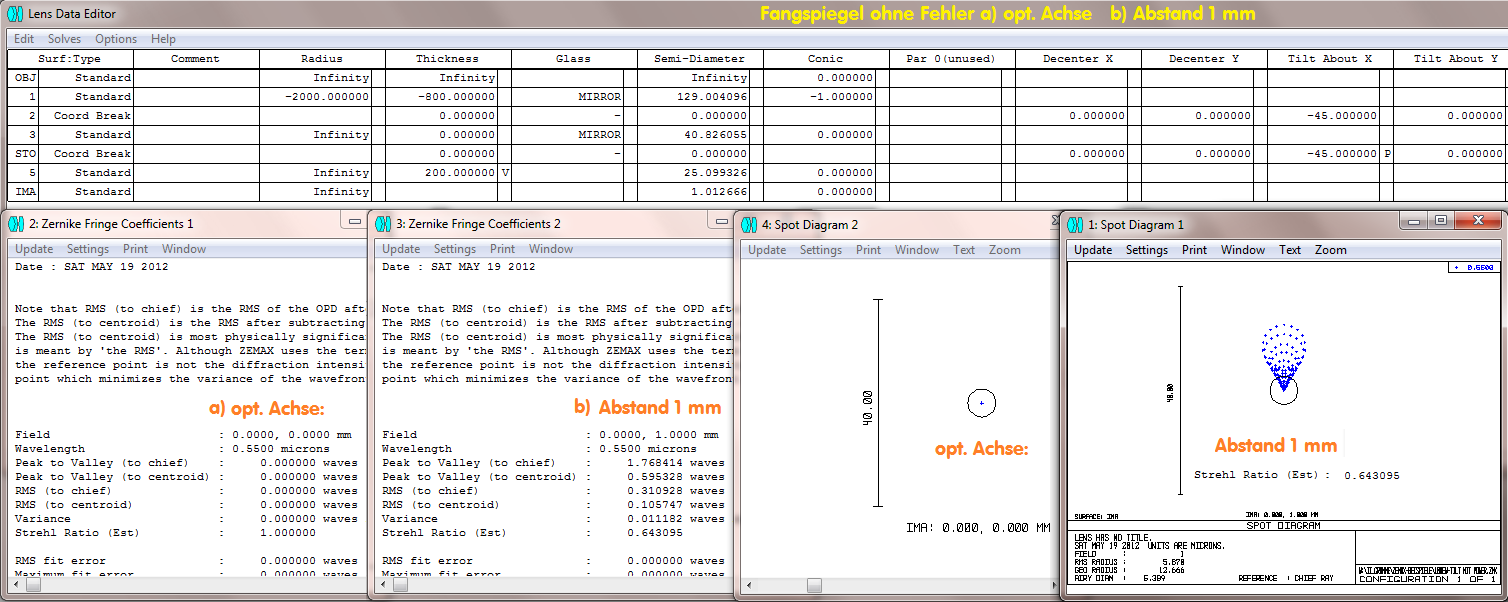
Ein Radius von 4 km würde bei diesem System einen PV-Wert von ca. L/4 der Wellenfront einführen, eine fehlerhafte Zentrierung erheblich mehr, in
diesem Fall PV 1.66*L

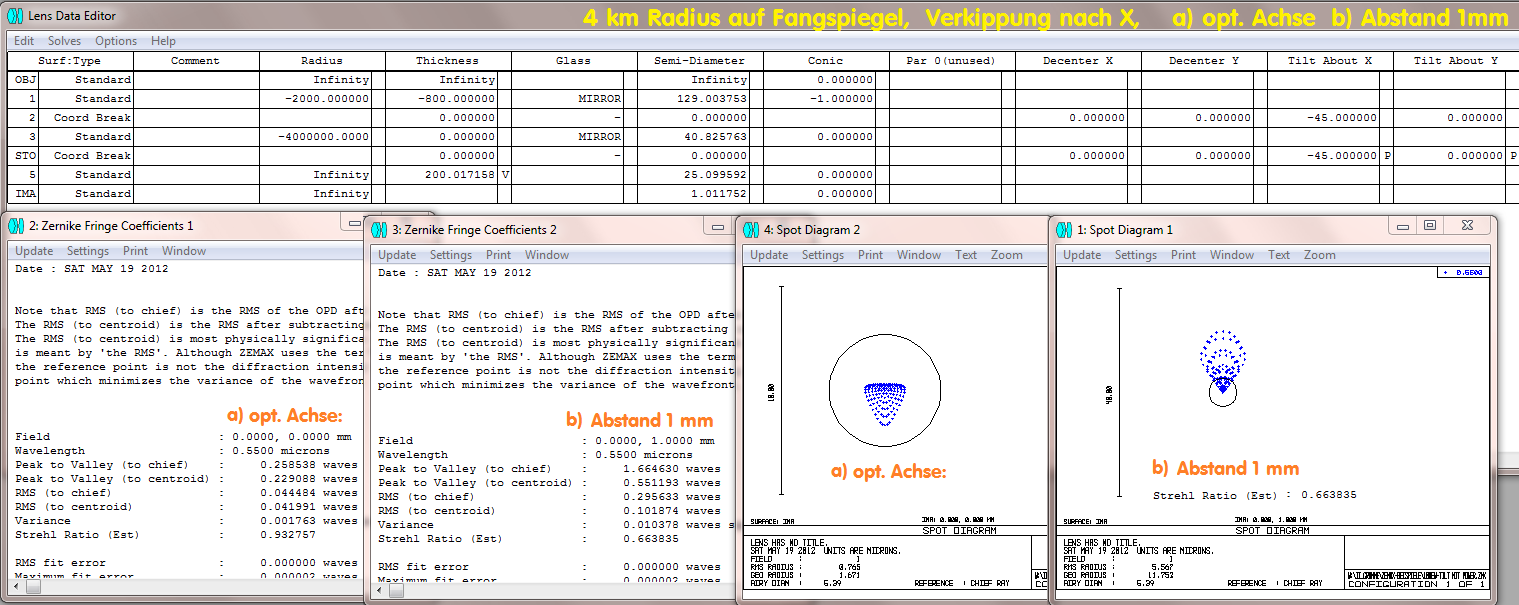
Da es eine "Sphäre" mit 4 km Radius ist, erzeugt die Verkippung in X bzw. Y zunächst die gleiche Fehlergröße. Lediglich bei Achsabstand 1 mm spielt die
Orientierung der Koma zum erzeugten Astigmatismus eine Rolle. Das ist auch der Grund, warum sich in einem begrenzten Bereich beim Newtonsystem
Koma gegen Astigmatismus (HS) ausspielen läßt.

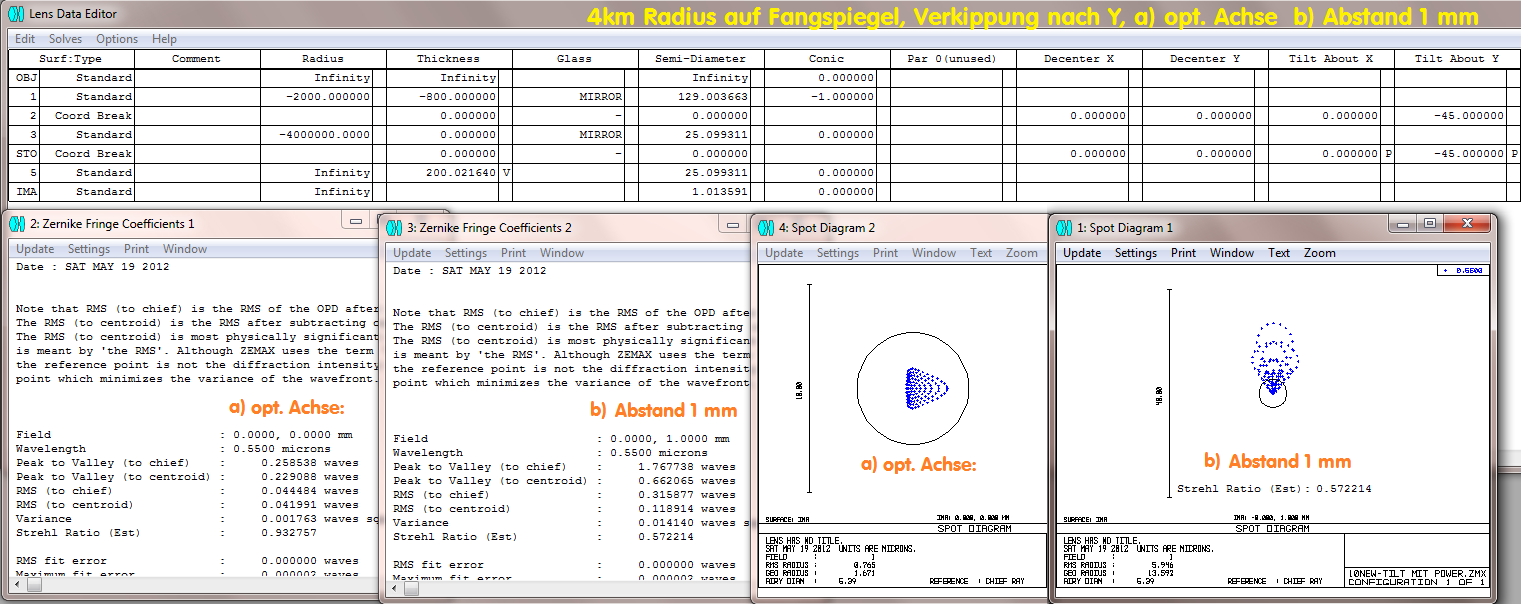
Wenn der Fangspiegel stattdessen torisch ist, dann spielt die Orientierung dieser Fläche eine Rolle: Quer zum Strahlengang wirkt sich der Fehler offenbar
stärker aus . . . .

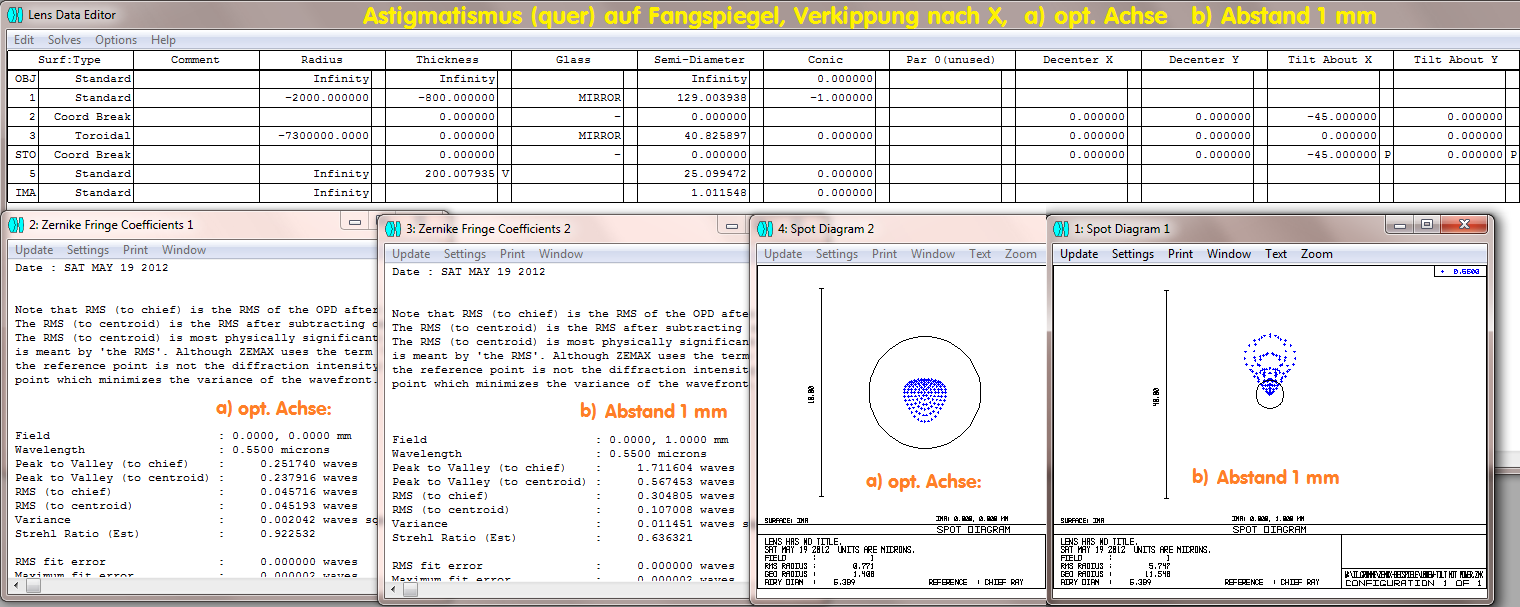
. . . . . während die Orientierung in Richtung Strahlengang (siehe Spotdiagramm jeweils auf der opt. Achse) einen kleineren Fehler erzeugt.

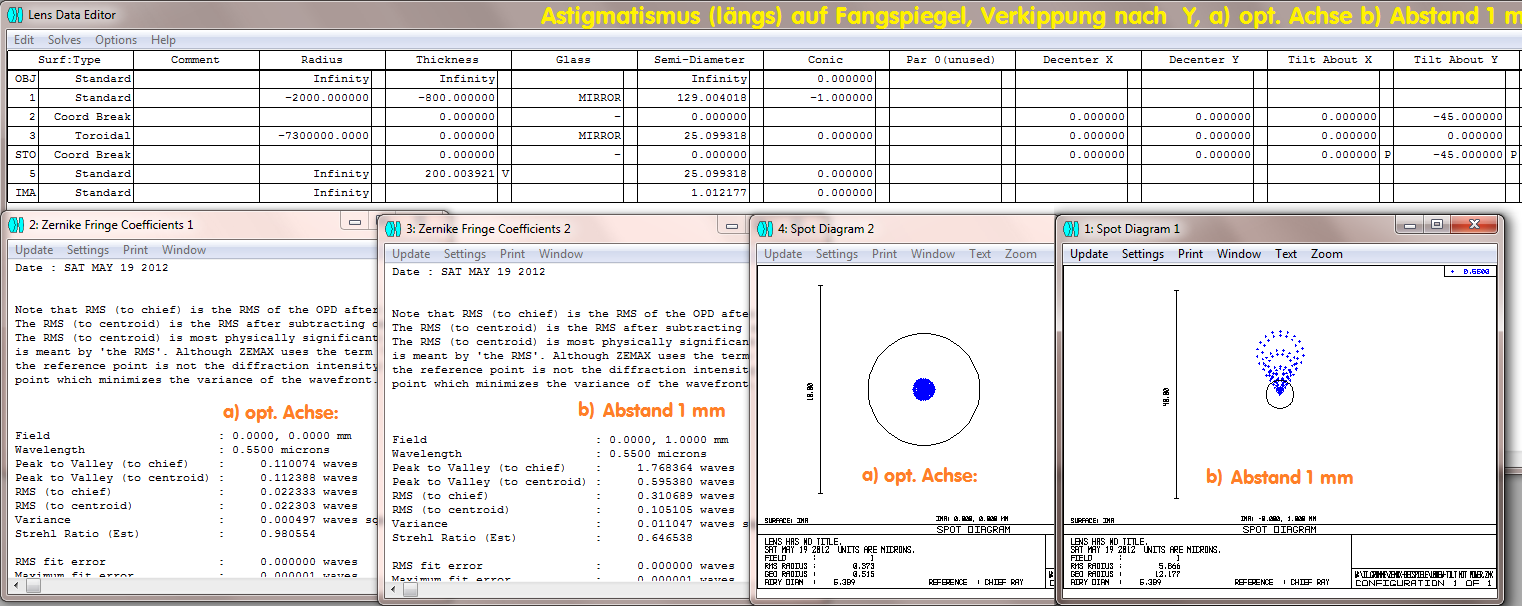
Fazit: F/4 Newton-Systeme reagieren auf Dezentrierung sehr viel kritscher, als auf Fehler, die der Fangspiegel einführt.

######################################################################################################################

sechs weitere Planspiegel im Test

Die Qualität von Fangspiegels scheint in der Praxis doch nicht so kritisch zu sein - wenn man sich die Erfahrungen von Händlern vergegenwärtigt.
Mithin ein Grund, über diesen Sachverhalt ein weiteres Mal zu berichten.
Zunächst muß man sehr deutlich unterscheiden zwischen Fangspiegeln, die bei der Feldfotografie eingesetzt werden und solchen für visuelle
Nutzung. Anspruchsvoller ist die zweite Variante. Wieviel der im Foto gezeigten jeweiligen Fangspiegel-Fläche wird denn optisch zur Abbildung eines
Punktes überhaupt gebraucht? Und immer nur genau diese Fläche muß einer Qualitäts-Norm von mindestens PV L/4 wave oder PV L/8 surface ent-
sprechen. Das gilt gleichermaßen für die Abbildung auf der opt. Achse, wie für die Sternabbildung im Bildfeld.

An folgendem Beispiel mag dies ersichtlich werden. Bei einem 10" Newtonspiegel f/5 (250/1250) ist bei 1 Meter vom Spiegel entfernt der Fangspiegel
plaziert, sodaß der Fokus mit 250 mm Abstand von der opt. Achse bequem außerhalb des Tubus zu liegen kommt und somit auch noch ein Koma-
Korrektor eingesetzt werden kann. (Dieses Beispiel fixiert nur eine bestimmte Situation und kann entsprechend variiert werden.)

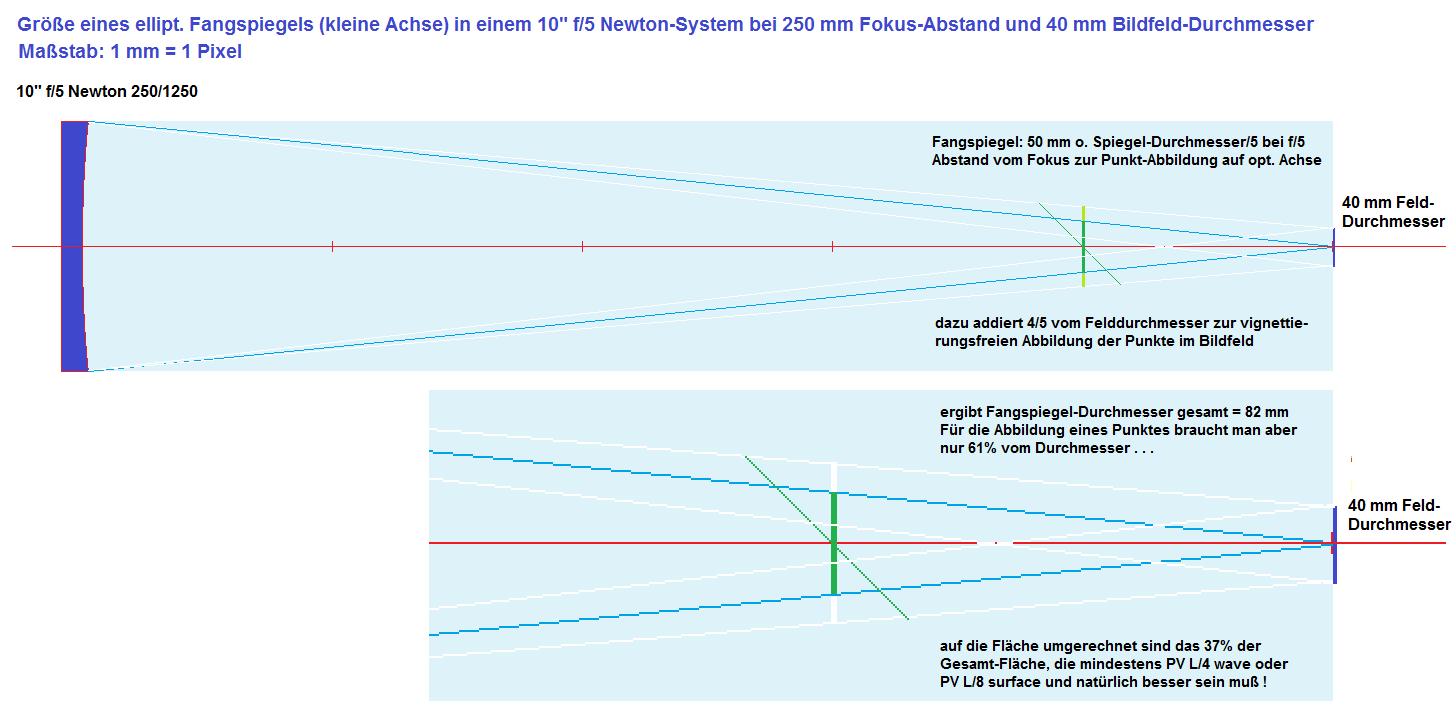
Diese Situation wurde maßstäblich so dargestellt, daß 1 Pixel 1 Millimenter entspricht. Im f/5 Lichtkegel, den dieser Spiegel erzeugt, haben wir bei einem Abstand von
1000 mm vom Newton-Spiegel einen Kegel-Durchmesser von 50 mm, was zur Abbildung eine Sterns auf der opt. Achse völlig ausreichend wäre. Im Bildfeld jedoch
hätten wir schnell die bekannte Vignettierung, die mit Helligkeitsabfall einhergeht. Der Fangspiegel am Ort 1000 mm muß also im Durchmesser größer sein als 50 mm.
Man muß also zunächst das gewünschte Bildfeld im Fokus selbst festlegen. In Anlehnung an das Kleinbildformat 24x36 mm ergäbe sich ein Bildfelddurchmesser
(Diagonale) von ca. 43.26 mm. Zugunsten einer einfacheren Rechnung nehme ich 40 mm als Bildfelddurchmesser.
Damit entsteht ein umgekehrter Kegel vom Fokus-Bildfeld-Durchmesser bis zur Mitte des Newton-Spiegels, der in der Höhe des Fangspiegels nur noch 32 mm Durch-
messer hat. Dieser Betrag muß also zu den 50 mm dazugezählt werden und man bekommt 82 mm Fangspiegel kleine Achse für die Position 1000 Abstand vom HS.
Damit läßt sich vignettierungsfrei das Bildfeld 40 mm im Fokus des 10" f/5 Newton ausleuchten.
Unabhängig davon braucht man für die Abbildung eines einzelnen Stern, wo immer er im Bildfeld ist, weiterhin den Fangspiegeldurchmesser von 50 mm.
Ein Prüf-Protokoll würde sich aber nun auf die Gesamtfläche des 82 mm Fangspiegels beziehen und gibt daher keinerlei Auskunft, wie tauglich dieser Spiegel in einem
bestimmten System überhaupt ist.

Diese Frage kann man nun auf mehrere Art beantworten:

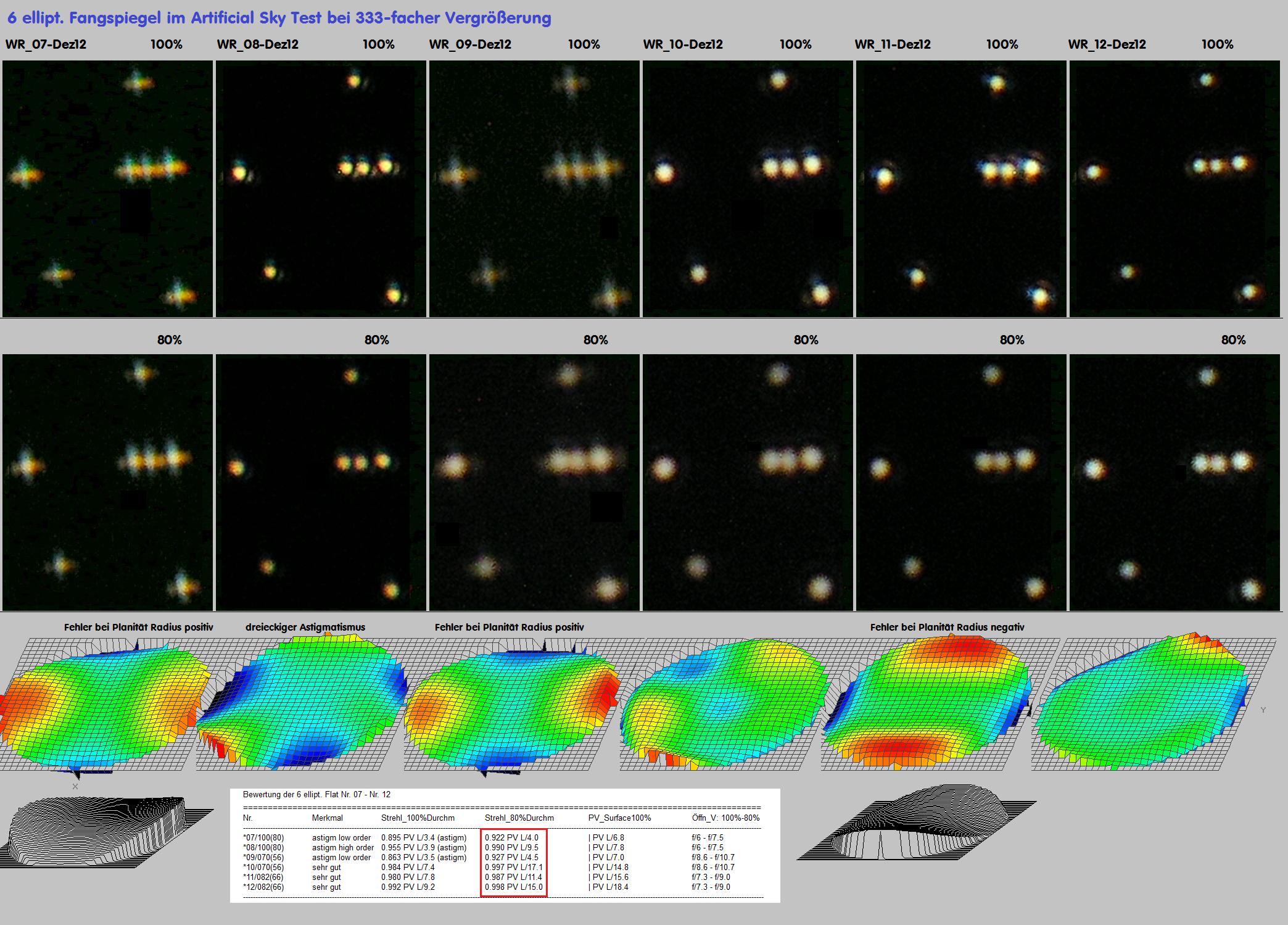
Mit Hilfe des Artificial Sky Testes (siehe die Berichte weiter oben) kann man in die Abbildung bei Höchstvergrößerung untersuchen und zwar a) über den vollen Durchmesser des
Fangspiegels und b) dem tatsächlich benutzen Durchmesser über die Einführung einer Blende. Bei der Auswertung der Interferogramme kann man ebenfalls a) den vollen Durch-
messer und b) einen prozentual verkleinerten Durchmesser auswerten, wobei ich hier von 80% des Gesamtdurchmessers ausgegangen bin, was bereits zu einer erheblichen
Qualitäts-Steigerung führt. Der Artificial Sky Test zeigt sofort einen vorhandenen Astigmatismus, der ein Hinweis auf fehlende Planität darstellt bzw. die Power. Bei mittlerer
Vergrößerung wird man diesen Sachverhalt eher schwer feststellen können.
Da dieser Test abhängig ist vom Radius 600 mm des Kugelspiegels ist, sind die Sternscheibchen-Durchmesser bei einem kleinen Spiegeldurchmesser entsprechend größer nach der
Formel: Auflösung (550 nm) = 138.40/D. Man muß also auch noch den Durchmessers des Fangspiegels berücksichtigen beim Betrachten der Testbilder.

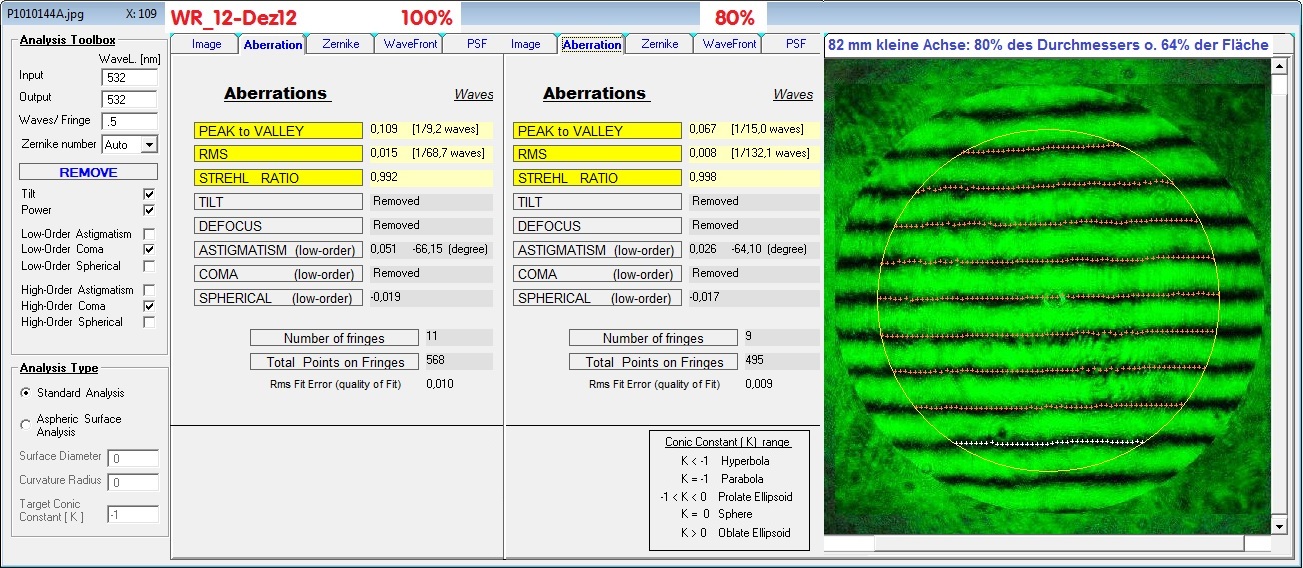
In Bild #4 sind die Ergebnisse von 100% Nenndurchmesser zu 80% Nenndurchmesser dargestellt. Der Umkreis von 100% wurde auf 80% reduziert, was nur noch 61% vom
Gesamtdurchmesser entspricht bzw. 50 mm. Auf die Fläche umgerechnet reduziert sich die Gesamtfläche auf nur noch 37% der Gesamtfläche, die man in diesem System tatsächlich
für die Abbildung eines Sternes braucht. Nun so ist es zu erklären, warum Fangspiegel von mittelmäßiger Qualität sich im praktischen Gebrauch sehr unauffällig zeigen.
.
.
.